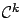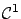Calculus of Variations and Optimal Control Theory A Concise Introduction

accessory equation

see Jacobi equation

action integral

adjoint system

3.4.2 | 4.2.8

adjoint vector

3.4.2 | 4.2.8 | 5.2 | see alsocostate

admissible perturbation

1.3.2

applications of optimal control

1.1 | 1.4

arclength

2.1.1

asymptotic stability

augmented cost

1.2.2.1 | 2.5.1 | 2.5.2

augmented system

4.2.1

bang-bang control

4.4.1 | 4.4.2

bang-bang principle

4.4.2 | 4.4.2 | 4.6

basic calculus of variations problem

2.2

basic fixed-endpoint control problem

4.1.1

basic variable-endpoint control problem

4.1.2

Bellman

5.1 | 5.1.5

Bernoulli, Johann

2.1.3 | 2.1.4

Bolza problem

3.3.2

boundary conditions

correct number of: 2.3.1 | 2.3.5 | 2.5.1 | 3.1.1 | 4.1.2

brachistochrone

2.1.4 | 2.7

Brouwer's fixed point theorem

4.2.6

canonical coordinates

canonical equations

2.4.1 | 3.4.2 | 7.1.3

as characteristics of HJB equation: 7.2.2

canonical variables

2.4.1

Carathéodory

5.1.5

Carathéodory

5.4

catenary

2.1.3 | 2.7 | 3.1.1 | 3.1.1

Cauchy initial value problem

7.2.1

Cauchy-Schwarz inequality

2.6.2

characteristic

7.2.1

characteristic strip

7.2.1

compactness

1.2.1.3 | 1.3.3 | 1.3.4

of reachable sets: 4.5 | 4.6

conjugate point

2.6.2

conservation law

conservative force

constrained optimization

1.2.2

constraint

equality: 1.2.2 | 4.1.2 | 7.1.1
holonomic: 2.5.2.1
integral: 2.5.1
non-integral: 2.5.2
nonholonomic: 2.5.2.1 | 2.7

contravariance

7.1.2

control set

1.1 | 3.3.1

control system

1.1 | 3.3.1

normal: 4.4.2
on a manifold: 7.1.2

controllability

4.4.2 | 4.6 | 6.2.1

convexity

1.2.1.3 | 1.2.1.3 | 1.3.4 | 1.4 | 4.2.7 | 4.5 | 7.3.3

coordinate chart

corner point

cost functional

1.1

augmented: 2.5.1 | 2.5.2
Bolza form: 3.3.2
Lagrange form: 3.3.2
Mayer form: 3.3.2

costate

3.4.2 | see alsoadjoint vector

as covector: 7.1.2

cotangent bundle

cotangent space

cotangent vector

see covector

covariance

covector

critical point

cycloid

Dido's isoperimetric problem

2.1.1

differentiable manifold

see manifold

differential game

5.1.5 | 7.3.2

differential of a function

7.1.1 | 7.1.2

disturbance attenuation

7.3.2

dual space

dynamic programming

5.1

discrete: 5.1.1

equality constraint

1.2.2 | 4.1.2 | 7.1.1

Erdmann

Euler

2.3.2

Euler-Lagrange equation

2.3.1

coordinate invariance: 2.3.3 | 2.7
for multiple degrees of freedom: 2.3.3
integral form: 2.3.3

existence and uniqueness of solution

existence of optimal solution

2.3.1 | 2.7 | 4.5 | 4.6

for Mayer problems: 4.5
for nonlinear time-optimal problems: 4.6

exponential stability

extremal

2.3.1

broken: 3.1.1

extremum

1.2 | 1.3.1

strong: 2.2.1
weak: 2.2.1

feasible direction

1.2.1.3

Fermat's principle

2.1.2

Filippov's theorem

4.5 | 4.6

final state

1.1 | 3.3.2

final time

1.1 | 3.3.2

finite escape time

2.6.2 | 6.1.4

finite-dimensional optimization

1.2

first variation

1.3.2

alternative definition: 1.3.2

first-order necessary condition

1.2.1.1 | 1.3.2

for constrained optimality: 1.2.2.1 | 2.5.1 | 2.5.2
for weak extremum: 2.3.1

fixed-time, free-endpoint problem

3.3.3

Fréchet derivative

1.3.2 | 1.4

free-time, fixed-endpoint problem

3.3.3

Fuller's phenomenon

4.4.4

Fuller's problem

4.4.4 | 4.6

function

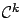
$\mathcal C^k$: 1.3.1
absolutely continuous: 3.3.1
locally Lipschitz: 3.3.1
measurable: 3.3.1
piecewise $\mathcal C^1$: 2.2.1
piecewise continuous: 3.3.1

functional

1.3

bilinear: 1.3.3
linear: 1.3.2
quadratic: 1.3.3

Gateaux derivative

1.3.2 | 1.4

global minimum

1.2 | 1.2.1.3 | 1.3.1 | 1.3.4

gradient

1.2.1.1

guard

see switching surface

Hamilton

2.4 | 5.1.5

Hamilton-Jacobi-Bellman (HJB) equation

5.1.3

and maximum principle: 5.2 | 7.2
characteristics of: 7.2.2
for infinite-horizon problems: 5.1.3.1
in calculus of variations: 5.1.5 | 5.4
solving: 5.4

Hamiltonian

2.3.4 | 2.4.1 | 3.4.1 | 4.1.1

as energy: 2.4.3
classical vs. modern formulation: 2.4.2

Hamiltonian matrix

6.1.1

Hamiltonian maximization condition

2.4.1 | 2.6.1 | 3.1.2 | 3.4.3 | 4.1.1 | 4.2.9.1 | 5.1.3

Hessian matrix

1.2.1.2

holonomic constraint

2.5.2.1

Hurwitz matrix

7.3.1

hybrid system

7.4

discrete state: 7.4.1

hyperplane

separating: 4.2.7 | 4.2.10
supporting: 4.4.2

infinite-dimensional optimization

1.3

infinite-horizon problem

3.3.3 | 5.1.3.1 | 6.2

integral constraint

2.5.1

inverse function theorem

Isaacs

5.1.5

Jacobi

2.6.2 | 5.1.5

Jacobi equation

2.6.2

Jacobian matrix

Kalman

5.1.5 | 6.3

Lagrange

1.2.2.1 | 2.2 | 2.3.2 | 2.5.1 | 2.6.2

Lagrange multiplier

1.2.2.1 | 2.5.1

distributed: 2.5.2

Lagrange problem

3.3.2

Lagrangian

2.2 | see alsorunning cost

augmented: 2.5.1 | 2.5.2
differentiability assumptions: 2.3.3 | 2.7

Legendre

2.6.1 | 2.6.2

Legendre transformation

2.4.2 | 2.7

Legendre's condition

2.6.1

for multiple degrees of freedom: 2.6.1 | 2.7

Legendre-Clebsch condition

3.4.3

light

reflection: 2.1.2 | 7.4.3
refraction: 2.1.2 | 2.1.4 | 2.7

linear matrix inequality (LMI)

7.3.3

linear quadratic regulator (LQR) problem

finite-horizon: 6.1
infinite-horizon: 6.2

linearization

3.4.1 | 4.2.4

Lipschitz condition

3.3.1 | 3.3.1

local coordinates

canonical: 7.1.1

local minimum

1.2 | 1.3.1

locally Lipschitz function

Lyapunov-like function

6.2.2 | 7.3.1

manifold

7.1

embedded: 7.1.1

maximum

1.2 | 1.3.1

vs. minimum: 1.2 | 2.2 | 3.4.4

maximum principle

and HJB equation: 5.2 | 7.2
for basic fixed-endpoint control problem: 4.1.1
for basic variable-endpoint control problem: 4.1.2
for fixed-time problems: 4.3.1.1
for Mayer problems: 4.6
for problems with terminal cost: 4.3.1.3
for time-varying problems: 4.3.1.2
higher-order: 4.6
hybrid: 7.4.2
in discrete time: 4.6
local optimality: 4.3 | 4.6
nonsmooth: 4.6
on manifolds: 7.1.2
sign convention: 3.4.4
stochastic: 4.6

Mayer problem

3.3.2

McShane

3.1.2 | 4.2.3

measurable function

minimum

global: 1.2 | 1.2.1.3 | 1.3.1 | 1.3.4
local: 1.2 | 1.3.1
strict: 1.2 | 1.3.1
vs. maximum: 1.2 | 2.2 | 3.4.4

momentum

2.3.4 | 2.4.1

angular: 2.4.3

multiple degrees of freedom

2.2

necessary condition

3.4.3 | see alsomaximum principle

first-order

1.2.1.1 | 1.3.2

for constrained optimality: 1.2.2.1 | 2.5.1 | 2.5.2
for weak extremum: 2.3.1

for strong extremum

for strong maximum

for strong minimum

second-order

1.2.1.2 | 1.3.3 | 2.6.1

for constrained optimality: 1.2.2.2

needle perturbation

4.2.3

Newton's second law

Noether's theorem

2.4.3 | 2.7

non-integral constraint

2.5.2

nonholonomic constraint

2.5.2.1 | 2.7

nontriviality condition

4.3

norm

1.3.1

normal system

4.4.2

observability

optimal control

1.1 | 3.3.3

bang-bang: 4.4.1 | 4.4.2
singular: 4.4.3

optimal control problem

1.1 | 3.3

Bolza form: 3.3.2
hybrid: 7.4.1
Lagrange form: 3.3.2
Mayer form: 3.3.2
on a manifold: 7.1.2

parking problem

4.4.1

partial differential equation (PDE)

5.1.3 | 5.3.2 | 7.2.1

pendulum

7.1

Perron's paradox

4.5

perturbation

admissible: 1.3.2
needle: 4.2.3
spatial: 4.2.3
temporal: 4.2.2

piecewise continuous function

Pontryagin

4.1.2 | 4.2.3

principle of least action

2.4.3 | 2.7

principle of optimality

4.2.1 | 5.1.2 | 5.1.5

quadratic form

1.3.3

reachable set

4.4.2 | 4.5

regular point

Riccati equation

algebraic

6.2.1

unique positive definite solution: 6.2.4

differential

2.6.2 | 2.6.2 | 6.1.2

global existence of solution: 6.1.4
reduction to linear differential equation: 2.6.2 | 2.6.2
solving: 6.3
steady-state solution: 6.2.1

Riccati inequality

7.3.1 | 7.3.2

reduction to LMI: 7.3.3

robust control

7.3.2

running cost

1.1 | 2.2 | 3.3.2

Schur complement

7.3.3

second variation

1.3.3

alternative definition: 1.3.3

second-order necessary condition

1.2.1.2 | 1.3.3 | 2.6.1

for constrained optimality: 1.2.2.2

second-order sufficient condition

1.2.1.2 | 1.3.3 | 2.6.2

for constrained optimality: 1.2.2.2

separating hyperplane

4.2.7 | 4.2.10

single degree of freedom

2.2

singular arc

4.4.3

Snell's law

2.1.2 | 2.1.4

spatial control perturbation

4.2.3

stability

state feedback

4.4.1 | 4.6 | 5.1.1 | 5.2 | 6.1.1

stationary point

1.2.1.1

strict minimum

1.2 | 1.3.1

strong extremum

2.2.1

sub-differential

5.3.1

suboptimal control

7.3.2

sufficient condition

1.2.1.2 | 1.3.3 | 3.4.4 | 5.1.4

for strong minimum: 3.1.2
for constrained optimality: 1.2.2.2
for strong minimum: 3.5
for weak minimum: 2.6.2

super-differential

5.3.1

supporting hyperplane

4.4.2

surface

1.2.1.3 | 1.2.1.3 | 4.1.2 | 7.1.1

switching condition

7.4.2

switching cost

7.4.1

switching curve

4.4.1 | 4.4.4

switching function

4.4.3

switching surface

7.4.1

switching time

7.4

symplectic form

7.1.3

tangent bundle

tangent space

1.2.2.1 | 7.1.1

characterization of: 1.2.2.1 | 1.4 | 4.1.2

tangent vector

target set

3.3.3

temporal control perturbation

4.2.2

terminal cone

4.2.5

terminal cost

1.1 | 3.3.2

terminal state

1.1 | 3.3.2

terminal time

1.1 | 3.3.2

test function

5.3.1

time-optimal problem

3.2 | 4.4 | 4.5 | 4.6

transition matrix

4.2.4

transversality condition

2.7 | 4.1.2 | 4.2.10

for Cauchy problem: 7.2.1
for initial sets: 4.3.1.4 | 7.4.2

unconstrained optimization

1.2.1

completely: 1.2.1

value function

5.1.2

as viscosity solution: 5.3.3
nondifferentiable: 5.2.1

variable initial state

4.3.1.4 | 7.4.1

variable-endpoint problem

4.1.2

in calculus of variations: 2.3.5 | 2.7

variation

alternative definition: 1.3.2 | 1.3.3
first: 1.3.2
second: 1.3.3

variational equation

2.6.2 | 4.2.4

viscosity

physical interpretation

5.3.2 | 5.4

solution

5.3.2

of HJB equation: 5.3.3

subsolution

5.3.2

supersolution

5.3.2

weak extremum

2.2.1

Weierstrass

3.1.1 | 3.1.2

Weierstrass excess function

Weierstrass necessary condition

Weierstrass theorem

1.2.1.3 | 1.3.4

Weierstrass-Erdmann corner conditions