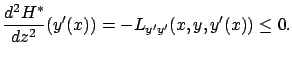Next: 2.6.2 Sufficient condition for
Up: 2.6 Second-order conditions
Previous: 2.6 Second-order conditions
Contents
Index
2.6.1 Legendre's necessary condition for a
weak minimum
Let us compute
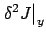 for a given test curve
for a given test curve  . Since third-order
partial
derivatives of
. Since third-order
partial
derivatives of 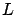 will appear, we assume that
will appear, we assume that
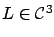 .
We work with the single-degree-of-freedom case for now.
The left-hand side of (2.56) is
.
We work with the single-degree-of-freedom case for now.
The left-hand side of (2.56) is
We need to write down its second-order Taylor expansion with respect
to 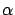 . We do this by expanding the function inside the integral
with respect to
. We do this by expanding the function inside the integral
with respect to 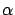 (using the chain rule) and separating the terms of different orders
in
(using the chain rule) and separating the terms of different orders
in 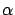 :
:
Matching
this expression with (2.56) term by term, we
deduce that the second
variation is given by
where the integrand is evaluated along
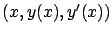 .
This is indeed a quadratic form as defined in Section 1.3.3.
Note that it explicitly depends on
.
This is indeed a quadratic form as defined in Section 1.3.3.
Note that it explicitly depends on 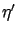 as well as on
as well as on 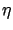 . In contrast
with the first variation (analyzed in detail in Section 2.3.1), the dependence of the second
variation on
. In contrast
with the first variation (analyzed in detail in Section 2.3.1), the dependence of the second
variation on 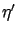 is essential and cannot be eliminated. We can, however,
simplify the expression for
is essential and cannot be eliminated. We can, however,
simplify the expression for
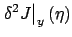 by eliminating the ``mixed"
term containing the product
by eliminating the ``mixed"
term containing the product 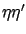 . We do this by using--as we did in our
earlier derivation of the Euler-Lagrange equation--the method of integration by parts:
. We do this by using--as we did in our
earlier derivation of the Euler-Lagrange equation--the method of integration by parts:
The first, non-integral term on the right-hand side vanishes due to the boundary
conditions (2.11). Therefore, the second variation can be written as
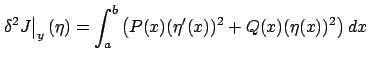 |
(2.56) |
where
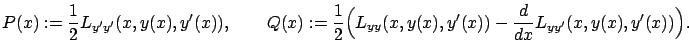 |
(2.57) |
Note that  is continuous, and
is continuous, and 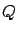 is also continuous at least when
is also continuous at least when
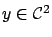 .
.
When we come to the issue of sufficiency in the next subsection, we will also need
a more precise characterization of the higher-order term labeled as
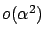 in the expansion (2.57).
The next exercise invites the reader to go back to the derivation of (2.57)
and analyze
this term in more detail.
in the expansion (2.57).
The next exercise invites the reader to go back to the derivation of (2.57)
and analyze
this term in more detail.

We know that if  is a minimum, then
for all
is a minimum, then
for all
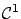 perturbations
perturbations 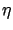 vanishing at the endpoints
the quantity (2.58)
must be nonnegative:
vanishing at the endpoints
the quantity (2.58)
must be nonnegative:
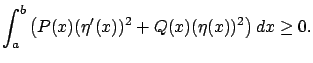 |
(2.58) |
We would like to restate this condition in terms of  and
and 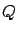 only--which
are defined directly from
only--which
are defined directly from 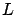 and
and  via (2.59)--so that we would
not
need to check it for all
via (2.59)--so that we would
not
need to check it for all 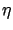 . (Recall that we followed a similar
route earlier when passing from the condition (2.16) to the
Euler-Lagrange equation via Lemma 2.1.)
. (Recall that we followed a similar
route earlier when passing from the condition (2.16) to the
Euler-Lagrange equation via Lemma 2.1.)
What, if anything,
does the inequality (2.61) imply about  and
and 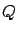 ?
Does it force at least one of these two functions, or perhaps both,
to be nonnegative on
?
Does it force at least one of these two functions, or perhaps both,
to be nonnegative on ![$ [a,b]$](img210.gif) ?
The two terms inside the integral in (2.61) are
of course not independent because
?
The two terms inside the integral in (2.61) are
of course not independent because 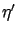 and
and
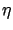 are related. So, we should try to see if maybe one of them
dominates the other.
More specifically, can it
happen that
are related. So, we should try to see if maybe one of them
dominates the other.
More specifically, can it
happen that 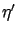 is large (in magnitude) while
is large (in magnitude) while 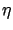 is small, or
the other way around?
is small, or
the other way around?
To answer these questions, consider a family of
perturbations
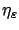 parameterized by small
parameterized by small
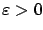 , depicted
in Figure 2.12. The function
, depicted
in Figure 2.12. The function
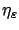 equals 0 everywhere outside some interval
equals 0 everywhere outside some interval
![$ [c,d]\subset[a,b]$](img567.gif) ,
and inside this interval it equals 1 except near the endpoints where it rapidly
goes up to 1 and back down to 0. This rapid transfer is accomplished by the
derivative
,
and inside this interval it equals 1 except near the endpoints where it rapidly
goes up to 1 and back down to 0. This rapid transfer is accomplished by the
derivative
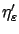 having a short pulse of width approximately
having a short pulse of width approximately
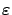 and height
approximately
and height
approximately
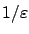 right after
right after 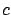 , and a similar negative pulse right before
, and a similar negative pulse right before
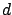 . Here
. Here
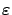 is small compared to
is small compared to 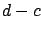 . We base
the subsequent argument on this graphical description, but it is
not difficult to specify a formula for
. We base
the subsequent argument on this graphical description, but it is
not difficult to specify a formula for
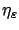 and use it to
verify the claims that follow; see, e.g., [GF63, p. 103] for a similar
construction.
and use it to
verify the claims that follow; see, e.g., [GF63, p. 103] for a similar
construction.
Figure:
The graphs of
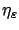 and its derivative
and its derivative
|
|
We can see that
and this bound is uniform over
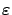 .
On the other hand, for nonzero
.
On the other hand, for nonzero  the integral
the integral
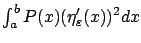 does not stay bounded as
does not stay bounded as
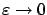 , because it is of order
, because it is of order
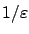 . In particular, let us see this more clearly for the case
when
. In particular, let us see this more clearly for the case
when  is negative on
is negative on ![$ [c,d]$](img374.gif) , so
that for some
, so
that for some 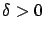 we have
we have
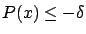 for all
for all ![$ x\in[c,d]$](img380.gif) . Assume
that there is an interval inside
. Assume
that there is an interval inside
![$ [c,c+\varepsilon ]$](img577.gif) of length at least
of length at least
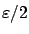 on which
on which
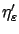 is no smaller than
is no smaller than
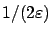 ; this property is
completely consistent
with our earlier description of
; this property is
completely consistent
with our earlier description of
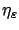 and
and
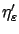 . We then have
. We then have
As
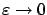 , the above expression tends to
, the above expression tends to 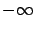 , dominating the
bounded
, dominating the
bounded 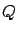 -dependent term.
It follows that the inequality (2.61) cannot hold for all
-dependent term.
It follows that the inequality (2.61) cannot hold for all
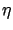 if
if  is negative on some subinterval
is negative on some subinterval ![$ [c,d]$](img374.gif) . But this means that for
. But this means that for
 to be a minimum,
to be a minimum,  must be nonnegative everywhere on
must be nonnegative everywhere on ![$ [a,b]$](img210.gif) . Indeed,
if
. Indeed,
if
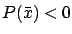 for some
for some
![$ \bar x\in[a,b]$](img373.gif) , then by continuity of
, then by continuity of  we can find a subinterval
we can find a subinterval ![$ [c,d]$](img374.gif) containing
containing 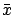 on which
on which  is negative,
and the above construction can be applied.2.3
is negative,
and the above construction can be applied.2.3
Recalling
the definition of  in (2.59), we arrive at our
second-order necessary condition for optimality: For all
in (2.59), we arrive at our
second-order necessary condition for optimality: For all ![$ x\in [a,b]$](img446.gif) we must have
we must have
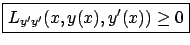 |
(2.59) |
This condition is known as Legendre's condition, as it was obtained by
Legendre in 1786.
Note that it places no restrictions on the sign of 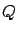 ; intuitively speaking,
the
; intuitively speaking,
the 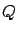 -dependent term in the second variation is dominated
by the
-dependent term in the second variation is dominated
by the  -dependent term, hence
-dependent term, hence 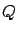 can in principle be negative along the
optimal curve (this point will become clearer in the next subsection).
For multiple degrees of freedom, the proof takes a bit more work but the statement of Legendre's
condition is virtually unchanged:
can in principle be negative along the
optimal curve (this point will become clearer in the next subsection).
For multiple degrees of freedom, the proof takes a bit more work but the statement of Legendre's
condition is virtually unchanged:
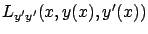 , which becomes a symmetric
matrix, must be positive semidefinite
for all
, which becomes a symmetric
matrix, must be positive semidefinite
for all  , i.e., (2.62) must hold
in the matrix sense along the optimal curve.
, i.e., (2.62) must hold
in the matrix sense along the optimal curve.
As a brief digression, let us recall our definition (2.29)
of the Hamiltonian:
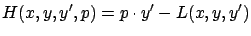 |
(2.60) |
where
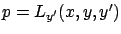 . We already noted in
Section 2.4.1 that when
. We already noted in
Section 2.4.1 that when 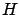 is viewed as a function
of
is viewed as a function
of 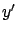 with the other
arguments evaluated along an optimal curve
with the other
arguments evaluated along an optimal curve  ,
it should have a stationary point
at
,
it should have a stationary point
at 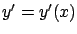 , the velocity of
, the velocity of  at
at  . More, precisely, the
function
. More, precisely, the
function 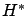 defined in (2.32) has a stationary point at
defined in (2.32) has a stationary point at
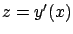 , which is a consequence of (2.33). Legendre's
condition tells us that, in addition,
, which is a consequence of (2.33). Legendre's
condition tells us that, in addition,
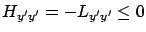 along an optimal curve, which we can rewrite in
terms of
along an optimal curve, which we can rewrite in
terms of 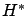 as
as
Thus, if the above stationary point is an extremum, then it is
necessarily a maximum.
This interpretation of necessary conditions
for optimality moves us one step closer to the maximum principle.
The basic idea behind our derivation of Legendre's condition will
reappear in Section 3.4 in the context of optimal
control, but eventually (in Chapter 4) we will obtain a
stronger result using more advanced techniques.





Next: 2.6.2 Sufficient condition for
Up: 2.6 Second-order conditions
Previous: 2.6 Second-order conditions
Contents
Index
Daniel
2010-12-20
![]() for a given test curve
for a given test curve ![]() . Since third-order
partial
derivatives of
. Since third-order
partial
derivatives of ![]() will appear, we assume that
will appear, we assume that
![]() .
We work with the single-degree-of-freedom case for now.
The left-hand side of (2.56) is
.
We work with the single-degree-of-freedom case for now.
The left-hand side of (2.56) is
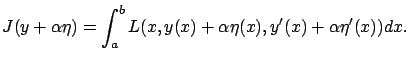
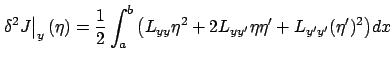
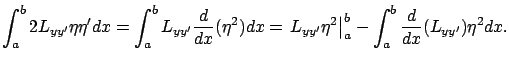
![]() in the expansion (2.57).
The next exercise invites the reader to go back to the derivation of (2.57)
and analyze
this term in more detail.
in the expansion (2.57).
The next exercise invites the reader to go back to the derivation of (2.57)
and analyze
this term in more detail.
![]() is a minimum, then
for all
is a minimum, then
for all
![]() perturbations
perturbations ![]() vanishing at the endpoints
the quantity (2.58)
must be nonnegative:
vanishing at the endpoints
the quantity (2.58)
must be nonnegative:
![]() and
and ![]() ?
Does it force at least one of these two functions, or perhaps both,
to be nonnegative on
?
Does it force at least one of these two functions, or perhaps both,
to be nonnegative on ![]() ?
The two terms inside the integral in (2.61) are
of course not independent because
?
The two terms inside the integral in (2.61) are
of course not independent because ![]() and
and
![]() are related. So, we should try to see if maybe one of them
dominates the other.
More specifically, can it
happen that
are related. So, we should try to see if maybe one of them
dominates the other.
More specifically, can it
happen that ![]() is large (in magnitude) while
is large (in magnitude) while ![]() is small, or
the other way around?
is small, or
the other way around?
![]() parameterized by small
parameterized by small
![]() , depicted
in Figure 2.12. The function
, depicted
in Figure 2.12. The function
![]() equals 0 everywhere outside some interval
equals 0 everywhere outside some interval
![]() ,
and inside this interval it equals 1 except near the endpoints where it rapidly
goes up to 1 and back down to 0. This rapid transfer is accomplished by the
derivative
,
and inside this interval it equals 1 except near the endpoints where it rapidly
goes up to 1 and back down to 0. This rapid transfer is accomplished by the
derivative
![]() having a short pulse of width approximately
having a short pulse of width approximately
![]() and height
approximately
and height
approximately
![]() right after
right after ![]() , and a similar negative pulse right before
, and a similar negative pulse right before
![]() . Here
. Here
![]() is small compared to
is small compared to ![]() . We base
the subsequent argument on this graphical description, but it is
not difficult to specify a formula for
. We base
the subsequent argument on this graphical description, but it is
not difficult to specify a formula for
![]() and use it to
verify the claims that follow; see, e.g., [GF63, p. 103] for a similar
construction.
and use it to
verify the claims that follow; see, e.g., [GF63, p. 103] for a similar
construction.
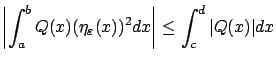
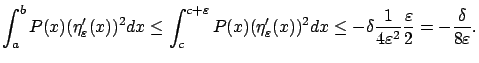
![]() in (2.59), we arrive at our
second-order necessary condition for optimality: For all
in (2.59), we arrive at our
second-order necessary condition for optimality: For all ![]() we must have
we must have