4.2.10 Transversality condition

We now turn to the Basic Variable-Endpoint Control Problem. In this case there is an additional statement to be proved, which is the transversality condition (4.3). In Section 4.2.6 we had that the terminal cone $C_{t^*}$ was separated from the ray $\vec\mu$ ; the reason for this was that hitting a point on $\vec\mu$ below $y^*(t^*)$ contradicted optimality. When the fixed endpoint $x_1$ is replaced by the surface $S_1$ , we would instead have a contradiction with optimality if we were able to hit a point with a cost lower than $x^{0,*}(t^*)$ whose $x$ -component is in $S_1$ (but is not necessarily $x^*(t^*)$ ). Let us denote the set of such points by $D$ . We are looking to establish separation between convex sets; for this reason, just as we replace the actual set of terminal points with its linear approximation $C_{t^*}$ , we will consider the linear approximation of $D$ given by the linear span of $\vec\mu$ and the tangent space $T_{x^*(t^*)}S_1$ , i.e., the set

$$T:=\left\{y\in\mathbb{R}^{n+1}:y=y^*(t^*)+\begin{pmatrix}{0}\\ {d}\end{pmatrix}+\beta\mu,\ d\in T_{x^*(t^*)}S_1,\, \beta\ge 0\right\}.$$ (4.37)

In Figure 4.12, $T$ is the shaded ``semi-plane." The subspace $T_{x^*(t^*)}S_1$ , when translated to $y^*(t^*)$ , gives the upper line in the figure. $D$ is the surface (more precisely, the open semi-surface) consisting of points which lie ``directly under" the upper curve in the figure. $T$ is tangent to $D$ along $\vec\mu$ ; both $T$ and $D$ are bounded from above but extend infinitely far down (and $T$ includes its upper boundary while $D$ does not).

Figure: Illustrating the construction of the set $T$

This lemma is proved by an appropriate generalization of the argument we used to prove Lemma 4.1. Suppose that the statement is not true. Then we can find a point in $T$ which is contained in $C_{t^*}$ together with some $\varepsilon$ -ball $B_\varepsilon$ around it. We can write this point as

$$\hat y_\varepsilon =y^*(t^*)+\varepsilon \begin{pmatrix}{0}\\ {d}\end{pmatrix}+\varepsilon \beta\mu$$

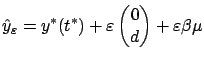
for suitable $d\in T_{x^*(t^*)}S_1$ and $\beta>0$ (moving $\hat y_\varepsilon$ slightly down if necessary, we can ensure that it does not lie on the upper boundary of $T$ ). Since $B_\varepsilon$ belongs to $C_{t^*}$ , each point in $B_\varepsilon$ is given by $y^*(t^*)+\varepsilon \nu$ where $\varepsilon \nu$ is a first-order terminal state perturbation arising from a temporal and/or spatial control perturbation. We know that the corresponding exact terminal states are of the form $y^*(t^*)+\varepsilon \nu+o(\varepsilon )$ and form a ``warped" version of $B_\varepsilon$ , which we denote by $\widetilde B_\varepsilon$ .

This construction remains valid as $\varepsilon \to 0$ . The ball $B_\varepsilon$ is centered at $\hat y_\varepsilon \in T$ , its radius is $\varepsilon$ , and the ``warping" that produces $\widetilde B_\varepsilon$ is of order $o(\varepsilon )$ . As in Exercise 4.5, it can be shown that $\widetilde B_\varepsilon$ contains a ball centered at $\hat y_\varepsilon$ whose radius is of order $\varepsilon -o(\varepsilon )$ . Furthermore, since $T$ and $D$ are tangent to each other along $\vec\mu$ , the distance from $\hat y_\varepsilon$ to $D$ is also of order $o(\varepsilon )$ . Hence, for $\varepsilon$ small enough, $\widetilde B_\varepsilon$ actually intersects $D$ . But this, as we already noted, contradicts optimality of $y^*$ , and the lemma is established. The preceding argument is illustrated in Figure 4.13, where the plane and the curved surface represent $T$ and $D$ , respectively, the shaded object is the portion of $\widetilde B_\varepsilon$ that lies between $T$ and $D$ , and the ray in $T$ containing $\hat y_\varepsilon$ , $\varepsilon >0$ is also shown.

Figure: Proving Lemma 4.2

By Lemma 4.2 and the Separating Hyperplane Theorem, there exists a hyperplane that separates $T$ and $C_{t^*}$ . We denote its normal vector by (4.28) as before. In view of the definition (4.37) of $T$ and the fact that $d=0$ belongs to $T_{x^*(t^*)}S_1$ , the separation property still gives us the inequalities (4.29) and (4.30). Thus all the constructions and conclusions of Sections 4.2.8 and 4.2.9 still apply, and so we know that the first three statements of the maximum principle are true. On the other hand, writing the separation property for vectors in $T$ with $\beta$ (the $\vec\mu$ -component) equal to 0, we obtain the additional inequality

$$\left\langle \begin{pmatrix}p_0^* \\ p^*(t^*) \end{pmatrix},\begi... ...ght\rangle=\langle p^*(t^*),d\rangle \ge 0\qquad\forall\, d\in T_{x^*(t^*)}S_1.$$ (4.38)

For each $d\in T_{x^*(t^*)}S_1$ we also have $-d\in T_{x^*(t^*)}S_1$ , as is clear from (4.4). This fact and (4.38) imply that actually $\langle p^*(t^*),d\rangle=0$ for all $d\in T_{x^*(t^*)}S_1$ , which is precisely the desired transversality condition (4.3). Figure 4.14 depicts $C_{t^*}$ , $T$ , and the separating hyperplane. Our proof of the maximum principle for the Basic Variable-Endpoint Control Problem is now complete.

Figure: A separating hyperplane for the Basic Variable-Endpoint Control Problem

Note that in the special case when $S_1=\mathbb{R}^n$ (a free-time, free-endpoint problem), the hyperplane must separate $C_{t^*}$ from the entire $(n+1)$ -dimensional half-space that lies below $y^*(t^*)$ . Clearly, this hyperplane must be horizontal, hence its normal must be vertical and we conclude that $p^*(t^*)=0$ . This is consistent with (4.3) because $T_{x^*(t^*)}S_1=\mathbb{R}^n$ in this case.