




Next: 1.3 Preview of infinite-dimensional
Up: 1.2.2 Constrained optimization
Previous: 1.2.2.1 First-order necessary condition
Contents
Index
For the sake of completeness, we quickly
state the second-order conditions for constrained optimality;
they will not be used
in the sequel.
For the necessary condition,
suppose that 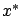 is a regular point of
is a regular point of 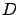 and a local minimum of
and a local minimum of 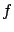 over
over 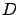 , where
, where 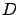 is defined by the equality
constraints (1.18) as before.
We let
is defined by the equality
constraints (1.18) as before.
We let 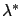 be the vector of Lagrange multipliers
provided by the first-order necessary
condition, and define the augmented
cost
be the vector of Lagrange multipliers
provided by the first-order necessary
condition, and define the augmented
cost 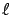 as in (1.27). We also assume that
as in (1.27). We also assume that 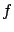 is
is
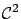 . Consider the Hessian of
. Consider the Hessian of 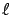 with respect to
with respect to  evaluated
at
evaluated
at
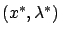 :
:
The second-order necessary condition says that
this Hessian matrix must be positive semidefinite on the tangent space to 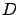 at
at 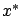 , i.e.,
we must have
, i.e.,
we must have
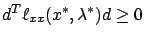 for all
for all
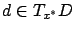 . Note that this is weaker than asking the above Hessian matrix
to be positive semidefinite in the usual sense
(on the entire
. Note that this is weaker than asking the above Hessian matrix
to be positive semidefinite in the usual sense
(on the entire
 ).
).
The second-order sufficient condition
says that a point 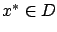 is a strict constrained local minimum of
is a strict constrained local minimum of 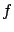 if
the first-order necessary condition for optimality (1.25) holds and,
in addition, we have
if
the first-order necessary condition for optimality (1.25) holds and,
in addition, we have
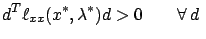 such that such that 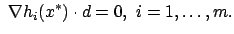 |
(1.29) |
Again, here 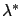 is the vector of Lagrange multipliers and
is the vector of Lagrange multipliers and 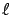 is the
corresponding augmented cost.
Note that
regularity of
is the
corresponding augmented cost.
Note that
regularity of 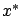 is not needed for this sufficient condition to be
true. If
is not needed for this sufficient condition to be
true. If 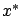 is in fact a
regular point, then we know (from our derivation of the first-order necessary
condition for constrained optimality) that the condition imposed on
is in fact a
regular point, then we know (from our derivation of the first-order necessary
condition for constrained optimality) that the condition imposed on 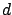 in (1.29) describes exactly the tangent vectors
to
in (1.29) describes exactly the tangent vectors
to 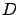 at
at 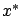 . In other words, in this case (1.29) is equivalent
to saying
that
. In other words, in this case (1.29) is equivalent
to saying
that
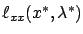 is positive definite on
the tangent space
is positive definite on
the tangent space 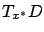 .
.





Next: 1.3 Preview of infinite-dimensional
Up: 1.2.2 Constrained optimization
Previous: 1.2.2.1 First-order necessary condition
Contents
Index
Daniel
2010-12-20
![]() is a regular point of
is a regular point of ![]() and a local minimum of
and a local minimum of ![]() over
over ![]() , where
, where ![]() is defined by the equality
constraints (1.18) as before.
We let
is defined by the equality
constraints (1.18) as before.
We let ![]() be the vector of Lagrange multipliers
provided by the first-order necessary
condition, and define the augmented
cost
be the vector of Lagrange multipliers
provided by the first-order necessary
condition, and define the augmented
cost ![]() as in (1.27). We also assume that
as in (1.27). We also assume that ![]() is
is
![]() . Consider the Hessian of
. Consider the Hessian of ![]() with respect to
with respect to ![]() evaluated
at
evaluated
at
![]() :
:
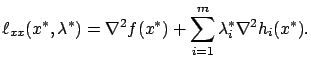
![]() is a strict constrained local minimum of
is a strict constrained local minimum of ![]() if
the first-order necessary condition for optimality (1.25) holds and,
in addition, we have
if
the first-order necessary condition for optimality (1.25) holds and,
in addition, we have