Let ![]() be a local minimum of
be a local minimum of ![]() over
over ![]() . We assume
that
. We assume
that ![]() is a regular point of
is a regular point of ![]() in the sense that
the gradients
in the sense that
the gradients
![]() ,
,
![]() are linearly independent
at
are linearly independent
at ![]() . This is a technical assumption needed to rule out degenerate
situations; see Exercise 1.2 below.
. This is a technical assumption needed to rule out degenerate
situations; see Exercise 1.2 below.
Instead of line segments containing ![]() which we used in the
unconstrained case, we now
consider curves in
which we used in the
unconstrained case, we now
consider curves in ![]() passing through
passing through ![]() . Such a curve is
a family of points
. Such a curve is
a family of points
![]() parameterized by
parameterized by
![]() , with
, with ![]() .
We require the function
.
We require the function ![]() to be
to be
![]() , at least for
, at least for ![]() near 0.
Given an arbitrary curve of this kind, we can consider the function
near 0.
Given an arbitrary curve of this kind, we can consider the function
Note that when there are no equality constraints, functions of the form (1.4) considered previously can be viewed as special cases of this more general construction. From the fact that 0 is a minimum of
which for
We want to have a more explicit characterization of the tangent space
![]() ,
which will help us understand it better. Since
,
which will help us understand it better. Since
![]() was defined as the set of points satisfying the equalities (1.18),
and since the points
was defined as the set of points satisfying the equalities (1.18),
and since the points ![]() lie in
lie in ![]() by construction,
we must have
by construction,
we must have
![]() for all
for all ![]() and all
and all
![]() . Differentiating
this formula gives
. Differentiating
this formula gives
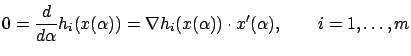
for all
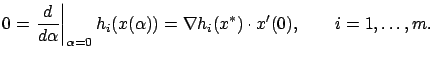
We have shown that for an arbitrary
Now let us go back to (1.19), which says
that
![]() for all
for all
![]() (since the
curve
(since the
curve ![]() and thus the tangent vector
and thus the tangent vector ![]() were arbitrary).
In view of the characterization of
were arbitrary).
In view of the characterization of ![]() given
by (1.20),
we can rewrite this condition as follows:
given
by (1.20),
we can rewrite this condition as follows:
Claim: The gradient of ![]() at
at ![]() is a linear combination of the
gradients of the constraint functions
is a linear combination of the
gradients of the constraint functions
![]() at
at ![]() :
:
Indeed, if the claim is not true, then
![]() has a component orthogonal to
span
has a component orthogonal to
span![]() , i.e, there exists a
, i.e, there exists a ![]() such that
such that
and we reach a contradiction with (1.21).
Geometrically, the claim says that
![]() is normal to
is normal to ![]() at
at ![]() .
This situation is illustrated in Figure 1.5 for the case
of two constraints in
.
This situation is illustrated in Figure 1.5 for the case
of two constraints in
![]() . Note that if there is only one constraint,
say
. Note that if there is only one constraint,
say ![]() , then
, then ![]() is a two-dimensional
surface and
is a two-dimensional
surface and
![]() must be proportional
to
must be proportional
to
![]() , the normal direction to
, the normal direction to ![]() at
at ![]() .
When the second constraint
.
When the second constraint ![]() is added,
is added, ![]() becomes a curve
(the thick curve
in the figure) and
becomes a curve
(the thick curve
in the figure) and
![]() is allowed to live in the plane spanned by
is allowed to live in the plane spanned by
![]() and
and
![]() , i.e., the normal plane to
, i.e., the normal plane to ![]() at
at ![]() .
In general, the intuition behind the claim is that
unless
.
In general, the intuition behind the claim is that
unless
![]() is normal to
is normal to ![]() ,
there are
curves in
,
there are
curves in ![]() passing through
passing through ![]() whose tangent vectors at
whose tangent vectors at ![]() make both positive and
negative inner products with
make both positive and
negative inner products with
![]() , hence in particular
, hence in particular ![]() can be decreased by moving away from
can be decreased by moving away from ![]() while staying in
while staying in ![]() .
.
The condition (1.22) means that there exist real numbers
![]() such that
such that
The above proof of the first-order necessary condition for constrained optimality involves geometric concepts. We also left a gap in it because we did not prove the converse implication in the equivalent characterization of the tangent space given by (1.20). We now give a shorter alternative proof which is purely analytic, and which will be useful when we study problems with constraints in calculus of variations. However, the geometric intuition behind the previous proof will be helpful for us later as well. We invite the reader to study both proofs as a way of testing the mathematical background knowledge that will be required in the subsequent chapters.
Let us start again by assuming that ![]() is a local minimum of
is a local minimum of ![]() over
over ![]() , where
, where
![]() is a surface in
is a surface in
![]() defined by the equality constraints (1.18) and
defined by the equality constraints (1.18) and ![]() is
a regular point of
is
a regular point of ![]() .
Our
goal is to rederive the necessary condition expressed by (1.25).
For
simplicity, we only give the argument for
the case of a single constraint
.
Our
goal is to rederive the necessary condition expressed by (1.25).
For
simplicity, we only give the argument for
the case of a single constraint ![]() , i.e.,
, i.e., ![]() ; the
extension to
; the
extension to ![]() is straightforward (see Exercise 1.3 below).
Given two arbitrary vectors
is straightforward (see Exercise 1.3 below).
Given two arbitrary vectors
![]() , we can consider the following map from
, we can consider the following map from
![]() to itself:
to itself:
The Jacobian matrix of
Regularity of ![]() in the present case just means that the gradient
in the present case just means that the gradient
![]() is nonzero.
Choose a
is nonzero.
Choose a ![]() such that
such that
![]() . With this
. With this ![]() fixed, let
fixed, let
![]() ,
so that
,
so that
![]() . Since the matrix (1.26) must be singular for all choices of
. Since the matrix (1.26) must be singular for all choices of ![]() , its first row must be a constant multiple of its second row (the second row being nonzero by our choice of
, its first row must be a constant multiple of its second row (the second row being nonzero by our choice of ![]() ). Thus we have
). Thus we have
![]() , or
, or
![]() , and this must be true for all
, and this must be true for all
![]() It follows that
It follows that
![]() , which proves (1.25) for the case when
, which proves (1.25) for the case when ![]() .
.
The first-order necessary condition for constrained optimality
generalizes the corresponding result we derived
earlier for the unconstrained case.
The condition (1.25) together with
the constraints (1.18) is a system of ![]() equations in
equations in ![]() unknowns:
unknowns: ![]() components of
components of ![]() plus
plus
![]() components of the Lagrange multiplier vector
components of the Lagrange multiplier vector
![]() . For
. For ![]() , we recover
the condition (1.11)
which consists of
, we recover
the condition (1.11)
which consists of ![]() equations in
equations in
![]() unknowns.
To make this relation even more explicit, consider the function
unknowns.
To make this relation even more explicit, consider the function
![]() defined by
defined by
The idea of passing from constrained minimization of the original cost function to
unconstrained minimization of the augmented cost function is due to Lagrange.
If
![]() is a minimum of
is a minimum of ![]() , then
we must
have
, then
we must
have ![]() (because otherwise we could decrease
(because otherwise we could decrease ![]() by changing
by changing ![]() ), and subject to these constraints
), and subject to these constraints
![]() should minimize
should minimize ![]() (because otherwise it would not minimize
(because otherwise it would not minimize
![]() ). Also, it is clear that (1.28) must hold. However,
it does not follow that (1.28) is a necessary condition
for
). Also, it is clear that (1.28) must hold. However,
it does not follow that (1.28) is a necessary condition
for ![]() to be a constrained minimum of
to be a constrained minimum of ![]() . Unfortunately, there is no quick way to
derive the first-order necessary condition for constrained optimality by
working with the augmented cost--something that Lagrange originally attempted to
do. Nevertheless, the basic form of the augmented cost function (1.27)
is fundamental in constrained optimization theory, and will
reappear in various forms several times in this book.
. Unfortunately, there is no quick way to
derive the first-order necessary condition for constrained optimality by
working with the augmented cost--something that Lagrange originally attempted to
do. Nevertheless, the basic form of the augmented cost function (1.27)
is fundamental in constrained optimization theory, and will
reappear in various forms several times in this book.
Even though the condition in terms of Lagrange multipliers is only necessary and not sufficient for constrained optimality, it is very useful for narrowing down candidates for local extrema. The next exercise illustrates this point for a well-known optimization problem arising in optics.