




Next: 7.3.2 control problem
Up: 7.3 Riccati equations and
Previous: 7.3 Riccati equations and
Contents
Index
We consider a linear time-invariant system
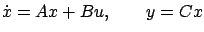 |
(7.17) |
and the cost functional
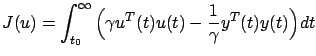 |
(7.18) |
with 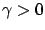 . In this cost, the squared norms of the input and the output inside the integral are multiplied by scalar weights of the opposite signs (and we assume the two weights to have been normalized so that their product equals
. In this cost, the squared norms of the input and the output inside the integral are multiplied by scalar weights of the opposite signs (and we assume the two weights to have been normalized so that their product equals 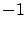 ). Consequently, it is clear that the optimal cost will now be nonpositive (just set
). Consequently, it is clear that the optimal cost will now be nonpositive (just set 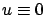 ). Nevertheless, as we will see, the form of the optimal solution
is very similar to the one we saw in Section 6.2 and can be
established using similar calculations.
Suppose that there exists a matrix
). Nevertheless, as we will see, the form of the optimal solution
is very similar to the one we saw in Section 6.2 and can be
established using similar calculations.
Suppose that there exists a matrix  with the following three properties:
with the following three properties:
-
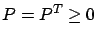 .
.
 is a solution of the ARE
is a solution of the ARE
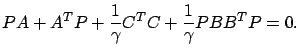 |
(7.19) |
- The matrix
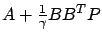 is Hurwitz.7.2
is Hurwitz.7.2
Then, we claim that the optimal cost is
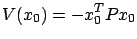 |
(7.20) |
and the optimal control is the linear state feedback
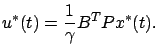 |
(7.21) |
(Notice the ``wrong" signs in the formulas (7.19)-(7.21) compared to Section 6.2; this sign difference could be reconciled by working with 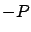 instead of
instead of  here.)
here.)
To prove this claim, let us define the function
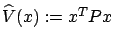 . Its derivative along solutions of the system (7.17) is
. Its derivative along solutions of the system (7.17) is
 , which is easily checked to be equivalent to
, which is easily checked to be equivalent to
 |
(7.22) |
We now
introduce the auxiliary finite-horizon cost
 |
(7.23) |
Using the formula (7.22) and noting that the first term on its right-hand side vanishes by (7.19), we can rewrite this cost as
which makes it clear that (7.20) and (7.21) are the optimal cost and optimal control for the cost functional (7.23). We want to show that they are also optimal for the original cost functional (7.18).
To this end,
we first note that
since  , the following bound holds for all
, the following bound holds for all  :
:
On the other hand, we can pass to the limit as
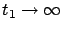 in the already established relation
in the already established relation
where 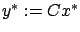 . In view of the fact that
. In view of the fact that
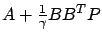 is a Hurwitz matrix, the closed-loop system
is a Hurwitz matrix, the closed-loop system
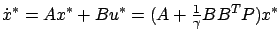 is exponentially stable. We thus obtain
is exponentially stable. We thus obtain
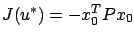 ,
and the desired result is proved.
,
and the desired result is proved.
While the formulas appearing here and in Section 6.2 are similar, the meanings of the two
problems are very different. The cost (7.18) no longer reflects the objective of keeping both  and
and  small. Instead, this cost is small when
small. Instead, this cost is small when  is large relative to
is large relative to  . We can regard
. We can regard  here not as a control that regulates the output but as a disturbance that tries to make the output large, with the optimal input being in some sense the worst-case disturbance. Let us try to formulate this idea in more precise terms. The fact that (7.20) is the optimal cost for the functional (7.18) implies that the inequality
here not as a control that regulates the output but as a disturbance that tries to make the output large, with the optimal input being in some sense the worst-case disturbance. Let us try to formulate this idea in more precise terms. The fact that (7.20) is the optimal cost for the functional (7.18) implies that the inequality
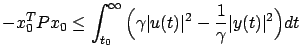 |
(7.24) |
holds for all  , with the equality achieved by the optimal control
, with the equality achieved by the optimal control 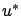 . From now on we focus on the case when
. From now on we focus on the case when 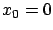 . Specializing (7.24) to this case, after simple manipulations we reach
. Specializing (7.24) to this case, after simple manipulations we reach
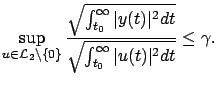 |
(7.25) |
The fraction on the left-hand side of (7.25) is the ratio of the
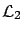 norms7.3 of the input and the output, and the supremum is being taken over all nonzero inputs with finite
norms7.3 of the input and the output, and the supremum is being taken over all nonzero inputs with finite
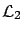 norms. If we
view the system (7.17), with the zero initial condition, as an input/output operator from
norms. If we
view the system (7.17), with the zero initial condition, as an input/output operator from
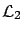 to
to
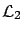 , then (7.25) says that the induced norm of this operator does not exceed
, then (7.25) says that the induced norm of this operator does not exceed 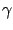 . This induced norm is called the
. This induced norm is called the
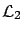 gain of the system.
gain of the system.
We see that if, for a given value of 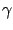 , we can find a matrix
, we can find a matrix  with the three properties listed at the beginning of this subsection, then the system's
with the three properties listed at the beginning of this subsection, then the system's
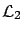 gain is less than or equal to
gain is less than or equal to 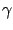 . (We do not know whether
. (We do not know whether 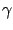 is actually achieved by some control; note that the optimal control (7.21) is excluded in (7.25) because it is identically 0 when
is actually achieved by some control; note that the optimal control (7.21) is excluded in (7.25) because it is identically 0 when 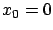 .) A converse result also holds: if the
.) A converse result also holds: if the
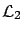 gain is less than
gain is less than 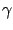 , then a matrix
, then a matrix  with the indicated properties exists. If we sidestep the original optimal control problem and only seek sufficient conditions for the
with the indicated properties exists. If we sidestep the original optimal control problem and only seek sufficient conditions for the
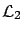 gain to be less than or equal to
gain to be less than or equal to 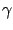 , then it is not hard to see from our earlier derivation that the conditions on the matrix
, then it is not hard to see from our earlier derivation that the conditions on the matrix  can be relaxed. Namely, it is enough to look for a symmetric positive semidefinite solution of the algebraic Riccati inequality
can be relaxed. Namely, it is enough to look for a symmetric positive semidefinite solution of the algebraic Riccati inequality
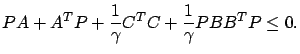 |
(7.26) |
The formula (7.22) then yields
Integrating both sides from 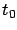 to an arbitrary time
to an arbitrary time 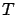 , rearranging terms,
and using the definition of
, rearranging terms,
and using the definition of
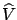 and the fact that
and the fact that 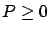 ,
we have
,
we have
and in the limit as
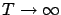 we again arrive at (7.25).
we again arrive at (7.25).
In the
frequency domain, the system (7.17) is characterized by the transfer matrix
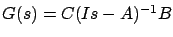 . Using Parseval's theorem, it can be shown that the
. Using Parseval's theorem, it can be shown that the
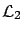 gain equals the largest singular value of
gain equals the largest singular value of
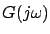 supremized over all frequencies
supremized over all frequencies
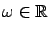 ; for systems with scalar inputs and outputs, this is just
; for systems with scalar inputs and outputs, this is just
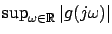 where
where 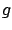 is the transfer function. In view of this fact, the
is the transfer function. In view of this fact, the
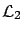 gain is also called the
gain is also called the
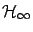 norm.
norm.





Next: 7.3.2 control problem
Up: 7.3 Riccati equations and
Previous: 7.3 Riccati equations and
Contents
Index
Daniel
2010-12-20
![]() . Its derivative along solutions of the system (7.17) is
. Its derivative along solutions of the system (7.17) is
![]() , which is easily checked to be equivalent to
, which is easily checked to be equivalent to
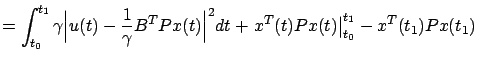
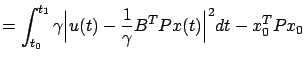
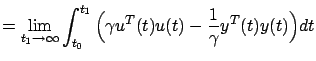
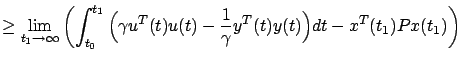
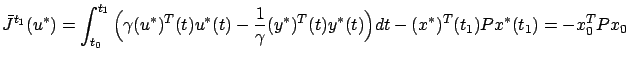
![]() and
and ![]() small. Instead, this cost is small when
small. Instead, this cost is small when ![]() is large relative to
is large relative to ![]() . We can regard
. We can regard ![]() here not as a control that regulates the output but as a disturbance that tries to make the output large, with the optimal input being in some sense the worst-case disturbance. Let us try to formulate this idea in more precise terms. The fact that (7.20) is the optimal cost for the functional (7.18) implies that the inequality
here not as a control that regulates the output but as a disturbance that tries to make the output large, with the optimal input being in some sense the worst-case disturbance. Let us try to formulate this idea in more precise terms. The fact that (7.20) is the optimal cost for the functional (7.18) implies that the inequality
![]() , we can find a matrix
, we can find a matrix ![]() with the three properties listed at the beginning of this subsection, then the system's
with the three properties listed at the beginning of this subsection, then the system's
![]() gain is less than or equal to
gain is less than or equal to ![]() . (We do not know whether
. (We do not know whether ![]() is actually achieved by some control; note that the optimal control (7.21) is excluded in (7.25) because it is identically 0 when
is actually achieved by some control; note that the optimal control (7.21) is excluded in (7.25) because it is identically 0 when ![]() .) A converse result also holds: if the
.) A converse result also holds: if the
![]() gain is less than
gain is less than ![]() , then a matrix
, then a matrix ![]() with the indicated properties exists. If we sidestep the original optimal control problem and only seek sufficient conditions for the
with the indicated properties exists. If we sidestep the original optimal control problem and only seek sufficient conditions for the
![]() gain to be less than or equal to
gain to be less than or equal to ![]() , then it is not hard to see from our earlier derivation that the conditions on the matrix
, then it is not hard to see from our earlier derivation that the conditions on the matrix ![]() can be relaxed. Namely, it is enough to look for a symmetric positive semidefinite solution of the algebraic Riccati inequality
can be relaxed. Namely, it is enough to look for a symmetric positive semidefinite solution of the algebraic Riccati inequality
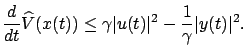
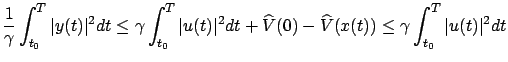
![]() . Using Parseval's theorem, it can be shown that the
. Using Parseval's theorem, it can be shown that the
![]() gain equals the largest singular value of
gain equals the largest singular value of
![]() supremized over all frequencies
supremized over all frequencies
![]() ; for systems with scalar inputs and outputs, this is just
; for systems with scalar inputs and outputs, this is just
![]() where
where ![]() is the transfer function. In view of this fact, the
is the transfer function. In view of this fact, the
![]() gain is also called the
gain is also called the
![]() norm.
norm.