4.2.7 Separating hyperplane

A standard result in convex analysis known as the Separating Hyperplane Theorem (see, e.g., [Ber99, Proposition B.13] or [BV04, Section 2.5.1]) says that if $C$ and $D$ are two nonempty disjoint convex sets then there exists a hyperplane that separates them; by this we mean that $C$ is contained in one of the two closed half-spaces created by the hyperplane and $D$ is contained in the other. The ray $\vec\mu$ is a convex set, and from the convexity of the terminal cone $C_{t^*}$ it is easy to see that its interior is convex as well. Lemma 4.1 guarantees that $\vec\mu$ does not intersect the interior of $C_{t^*}$ . Therefore, we can apply the Separating Hyperplane Theorem to conclude the existence of a hyperplane separating $\vec\mu$ from the interior of $C_{t^*}$ , and hence from $C_{t^*}$ itself.^4.3Obviously, this separating hyperplane must pass through the point $y^*(t^*)$ which is a common point of $C_{t^*}$ and $\vec\mu$ . Such a hyperplane need not be unique. The normal to the hyperplane is a nonzero vector in $\mathbb{R}^{n+1}$ (it is defined up to a constant multiple once we fix the hyperplane). Let us denote this normal vector by

$$\begin{pmatrix}p_0^* \\ p^*(t^*) \end{pmatrix}$$ (4.28)

where $p_0^*\in\mathbb{R}$ and $p^*(t^*)\in\mathbb{R}^n$ are, by definition, its $x^0$ -component and $x$ -component, respectively. Then the equation of the hyperplane is

$$\left\langle\begin{pmatrix} p_0^* \\ p^*(t^*) \end{pmatrix},y... ...angle\begin{pmatrix} p_0^* \\ p^*(t^*) \end{pmatrix},y^*(t^*)\right\rangle$$

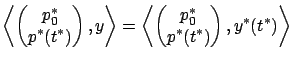
and the separation property is formally written as

$$\left\langle\begin{pmatrix}p_0^* \\ p^*(t^*) \end{pmatrix},\delta\right\rangle\le 0\qquad\forall\, \delta \ \, y^*(t^*)+\delta\in C_{t^*}$$ (4.29)

and

$$\left\langle\begin{pmatrix}p_0^* \\ p^*(t^*) \end{pmatrix},\mu\right\rangle\ge 0$$ (4.30)

where $\mu$ is the vector (4.26) which generates the ray $\vec\mu$ . Note that if we were to flip the direction of the normal vector (4.28), the inequality signs in (4.29) and (4.30) would be reversed; the present choice is simply a matter of sign convention (cf. Section 3.4.4). For an illustration, see Figure 4.11 in which the shaded object represents the separating hyperplane.

Figure: A separating hyperplane for the Basic Fixed-Endpoint Control Problem

In view of the definition (4.26) of $\mu$ , the inequality (4.30) simply says that $p_0^*\le 0$ , as required by the statement of the maximum principle. This will be the only use of (4.30). The normal vector (4.28) will serve as the terminal condition for the adjoint system, to be defined next.