




Next: 4.2.9 Properties of the
Up: 4.2 Proof of the
Previous: 4.2.7 Separating hyperplane
Contents
Index
4.2.8 Adjoint equation
As we already mentioned on page ![[*]](crossref.gif) , two (time-varying) linear systems of the form
, two (time-varying) linear systems of the form 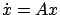 and
and
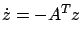 are called adjoint to each other. Solutions of adjoint systems are linked by the property that their inner product
are called adjoint to each other. Solutions of adjoint systems are linked by the property that their inner product
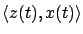 remains
constant, as shown by the following simple calculation:
remains
constant, as shown by the following simple calculation:
We now consider a specific pair of adjoint systems on the time
interval ![$ [t_0,t^*]$](img1168.gif) . As the first system (the
. As the first system (the  -system in the
above discussion) we take the variational
equation (4.19), described in more detail by the
equations (4.20) and (4.21). The second,
adjoint system is then
-system in the
above discussion) we take the variational
equation (4.19), described in more detail by the
equations (4.20) and (4.21). The second,
adjoint system is then
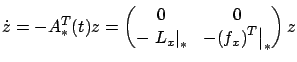 |
(4.31) |
where in the last expression, obtained from (4.21), 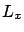 is a column vector (it is the gradient of
is a column vector (it is the gradient of 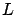 with respect to
with respect to  ) and
) and
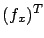 is the transpose of the Jacobian matrix of
is the transpose of the Jacobian matrix of 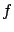 with respect to
with respect to  .
Let us denote the first component of
.
Let us denote the first component of 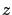 by
by 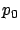 and the vector of the remaining
and the vector of the remaining 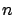 components of
components of 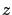 by
by 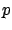 . Then the first differential equation in (4.31) reads
. Then the first differential equation in (4.31) reads
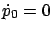 while the rest of the system (4.31) becomes
while the rest of the system (4.31) becomes
which, in view of the definition (4.2) of the Hamiltonian,
is equivalent to
Now, let us specify the terminal condition for the
system (4.31) at time 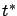 by setting
by setting 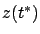 equal to
the vector (4.28). Further, we relabel the
equal to
the vector (4.28). Further, we relabel the
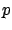 -component of the solution
-component of the solution 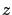 corresponding to this terminal
condition as
corresponding to this terminal
condition as 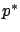 . This gives
. This gives
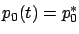 for all
for all 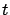 and
and
which is the second canonical equation in (4.1). With
a slight abuse of terminology, we will sometimes refer to this
differential equation as the adjoint equation. It is easy to see that the
first canonical equation in (4.1) also holds by the
definition of 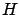 ; thus statement 1 of the maximum
principle has been established. By the aforementioned property of
adjoint systems, we have
; thus statement 1 of the maximum
principle has been established. By the aforementioned property of
adjoint systems, we have
![$\displaystyle \left\langle \begin{pmatrix}{p_0^*}\\ {p^*(t)}\end{pmatrix},\psi(...
...\\ {p^*(t^*)}\end{pmatrix},\psi(t^*)\right\rangle \qquad\forall\, t\in[t_0,t^*]$](img1214.gif) |
(4.32) |
for every solution 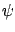 of the variational equation (4.19).
of the variational equation (4.19).
The vector (4.28), which is normal to the separating hyperplane,
is nonzero. Since (4.31)
is a homogeneous (unforced) linear time-varying system, we have
![$\displaystyle \begin{pmatrix}p_0^* \\ p^*(t) \end{pmatrix}\ne 0\qquad \forall\,t\in[t_0,t^*]$](img1215.gif) |
(4.33) |
as required in the statement of the maximum principle.
Geometrically, we can think of the vector in (4.33)
as the normal vector to a hyperplane passing through 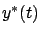 . We
can then associate the solution of the adjoint system to a family
of hyperplanes that is ``flowing back" along the optimal
trajectory. In view of (4.32), the perturbed
trajectory associated with
. We
can then associate the solution of the adjoint system to a family
of hyperplanes that is ``flowing back" along the optimal
trajectory. In view of (4.32), the perturbed
trajectory associated with 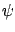 always remains on the same side
of the hyperplane.
always remains on the same side
of the hyperplane.





Next: 4.2.9 Properties of the
Up: 4.2 Proof of the
Previous: 4.2.7 Separating hyperplane
Contents
Index
Daniel
2010-12-20
![[*]](crossref.gif) , two (time-varying) linear systems of the form
, two (time-varying) linear systems of the form ![[*]](crossref.gif) , two (time-varying) linear systems of the form
, two (time-varying) linear systems of the form ![]() and
and
![]() are called adjoint to each other. Solutions of adjoint systems are linked by the property that their inner product
are called adjoint to each other. Solutions of adjoint systems are linked by the property that their inner product
![]() remains
constant, as shown by the following simple calculation:
remains
constant, as shown by the following simple calculation: 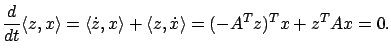
![]() . As the first system (the
. As the first system (the ![]() -system in the
above discussion) we take the variational
equation (4.19), described in more detail by the
equations (4.20) and (4.21). The second,
adjoint system is then
-system in the
above discussion) we take the variational
equation (4.19), described in more detail by the
equations (4.20) and (4.21). The second,
adjoint system is then