4.2 Proof of the maximum principle

Our proof of the two versions of the maximum principle stated in the previous section will be divided into the following steps.

Step 1: From Lagrange to Mayer form

As the first step, we will pass from the given Lagrange problem to an equivalent problem in the Mayer form by appending an additional state (this technique was already discussed in Section 3.3.2).

Step 2: Temporal control perturbation

In the next step, we will apply a small perturbation to the length of the time interval over which the optimal control is acting, and will characterize the resulting perturbation of the terminal state.

Step 3: Spatial control perturbation

In this step, we will replace the optimal control on a small time interval by an arbitrary constant control, and will study how the resulting state trajectory deviates from the optimal one at the end of this time interval. (This perturbation will be reminiscent of the one we used in the proof of the Weierstrass necessary condition in Section 3.1.2.)

Step 4: Variational equation

We will then derive a linear differential equation which propagates, modulo terms of higher order, the effect of spatial control perturbations up to the terminal time. This is the variational equation (we already encountered this terminology in Section 2.6.2).

Step 5: Terminal cone

Combining the effects of temporal and spatial control perturbations, we will construct a convex cone, with vertex at the terminal state of the optimal trajectory, which describes infinitesimal directions of all possible perturbations of the terminal state.

Step 6: Key topological lemma

Next, we will use optimality to show that the terminal cone does not contain in its interior the direction of decreasing cost.

Step 7: Separating hyperplane

We will invoke the separating hyperplane theorem to establish the existence of a hyperplane that passes through the terminal state and separates the terminal cone from the direction of decreasing cost. We will define the adjoint vector at the terminal time as the normal to this separating hyperplane.

Step 8: Adjoint equation

We will then introduce the adjoint equation which propagates the adjoint vector up to the terminal time; it will match the second canonical equation, as required by the maximum principle.

Step 9: Properties of the Hamiltonian

We will verify that the Hamiltonian maximization condition holds and that the Hamiltonian is identically 0 along the optimal trajectory. This will conclude the proof of the maximum principle for the Basic Fixed-Endpoint Control Problem.

Step 10: Transversality condition

Finally, we will prove the maximum principle for the Basic Variable-Endpoint Control Problem by refining the separation property from steps 6 and 7 and arriving at the transversality condition.

Each of the subsections that follow corresponds to one step in the proof. Until we reach step 10 in Section 4.2.10, we assume that we are dealing with the Basic Fixed-Endpoint Control Problem, i.e., 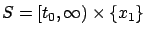$S=[t_0,\infty)\times\{x_1\}$ . The next exercise is meant to be worked on in parallel with following the proof.