




Next: 4.2.5 Terminal cone
Up: 4.2 Proof of the
Previous: 4.2.3 Spatial control perturbation
Contents
Index
4.2.4 Variational equation
We are now interested in how the difference between the trajectory
 arising from a spatial (needle) perturbation and the optimal trajectory
arising from a spatial (needle) perturbation and the optimal trajectory
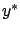 propagates after the perturbation stops acting, i.e., for
propagates after the perturbation stops acting, i.e., for 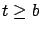 .
To study this question, let us
begin by writing
.
To study this question, let us
begin by writing
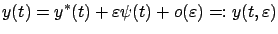 |
(4.16) |
for
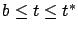 , where
, where
![$ \psi:[b,t^*]\to\mathbb{R}^{n+1}$](img1095.gif) is a quantity that we want to characterize and
is a quantity that we want to characterize and
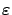 is the same as in Section 4.2.3. We know from (4.14) that
is the same as in Section 4.2.3. We know from (4.14) that 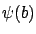 exists and is given by
exists and is given by
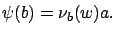 |
(4.17) |
We now derive a differential equation that 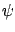 must satisfy on the time interval
must satisfy on the time interval ![$ (b,t^*]$](img1099.gif) , where both
, where both  and
and 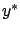 have the same corresponding control
have the same corresponding control 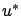 . It is clear from (4.16) that
. It is clear from (4.16) that
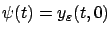 |
(4.18) |
(the existence of this partial derivative, and therefore of 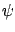 , for
, for 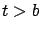 will become evident in a moment).
Let us rewrite the system (4.7) as an integral equation:
will become evident in a moment).
Let us rewrite the system (4.7) as an integral equation:
Differentiating both sides of this equation with respect to
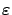 at
at
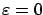 and using (4.16) with
and using (4.16) with 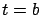 and (4.17),
we obtain
and (4.17),
we obtain
which, in view of (4.16) and (4.18), amounts to
Taking the derivative with respect to 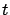 , we conclude that
, we conclude that 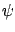 satisfies the differential equation
satisfies the differential equation
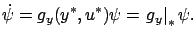 |
(4.19) |
We will use this equation to describe
how spatial perturbations propagate with time.
Pictorially, the role of 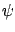 is illustrated
in Figure 4.6, with the understanding that the labels
involving
is illustrated
in Figure 4.6, with the understanding that the labels
involving 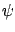 are accurate only up to terms of order
are accurate only up to terms of order
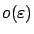 .
.
Figure:
Propagation of a spatial perturbation
|
|
The equation (4.19) can be written in the form
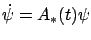 |
(4.20) |
where
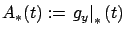 . This system is simply the
linearization of the original system (4.7) around
the optimal trajectory
. This system is simply the
linearization of the original system (4.7) around
the optimal trajectory 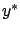 . Recall that a more detailed description of the system (4.7) is given by (4.5). Letting
. Recall that a more detailed description of the system (4.7) is given by (4.5). Letting
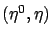 be the corresponding components of
be the corresponding components of 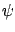 and writing out the variational equation (4.19) in terms of these
components, we easily arrive at
and writing out the variational equation (4.19) in terms of these
components, we easily arrive at
(because 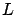 and
and 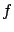 do not depend on
do not depend on 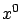 ). Here
). Here
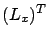 is a row vector (the transpose of the gradient of
is a row vector (the transpose of the gradient of 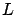 with respect to
with respect to  ) and
) and
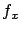 is an
is an 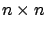 matrix (the Jacobian matrix of
matrix (the Jacobian matrix of 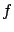 with respect to
with respect to  ). The resulting more explicit formula for
). The resulting more explicit formula for 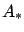 is
is
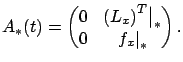 |
(4.21) |
The equation (4.19) is
in fact the variational equation corresponding to the system (4.7), according to the terminology
introduced in Section 2.6.2. The equation (3.27) in Section 3.4 is also similar and was similarly derived, although it served a different purpose (it described the effect of a small
control perturbation on a given trajectory, while here we are studying
the difference between two nearby trajectories with the same control).
Also, we see that
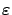 in the definition of a
needle perturbation
essentially corresponds to
in the definition of a
needle perturbation
essentially corresponds to 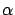 in the variational approach; we chose to use different symbols for these two parameters because of the different specific ways in which they are introduced.
in the variational approach; we chose to use different symbols for these two parameters because of the different specific ways in which they are introduced.
The value of 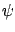 at the terminal time
at the terminal time 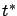 gives us an approximation of the terminal point
gives us an approximation of the terminal point 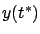 of the perturbed trajectory. Namely, from (4.16) evaluated
at
of the perturbed trajectory. Namely, from (4.16) evaluated
at 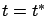 we have
we have
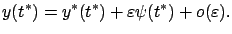 |
(4.22) |
Let us denote by
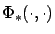 the transition
matrix for the linear time-varying system (4.20), so that
the transition
matrix for the linear time-varying system (4.20), so that
The initial value 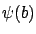 is given by (4.17),
hence
is given by (4.17),
hence
where 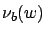 was defined in (4.15).
Plugging this expression into (4.22), we obtain
was defined in (4.15).
Plugging this expression into (4.22), we obtain
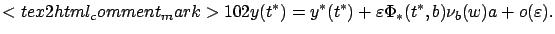 |
(4.23) |
Let us introduce the notation
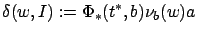 |
(4.24) |
to arrive at the more compact formula
(here the interval 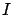 used for constructing the needle perturbation encodes information about the values of
used for constructing the needle perturbation encodes information about the values of 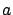 and
and 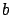 ).
).





Next: 4.2.5 Terminal cone
Up: 4.2 Proof of the
Previous: 4.2.3 Spatial control perturbation
Contents
Index
Daniel
2010-12-20
![]() arising from a spatial (needle) perturbation and the optimal trajectory
arising from a spatial (needle) perturbation and the optimal trajectory
![]() propagates after the perturbation stops acting, i.e., for
propagates after the perturbation stops acting, i.e., for ![]() .
To study this question, let us
begin by writing
.
To study this question, let us
begin by writing
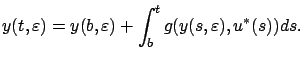
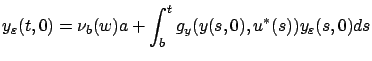
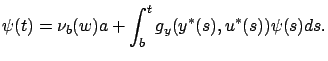
![]() in the definition of a
needle perturbation
essentially corresponds to
in the definition of a
needle perturbation
essentially corresponds to ![]() in the variational approach; we chose to use different symbols for these two parameters because of the different specific ways in which they are introduced.
in the variational approach; we chose to use different symbols for these two parameters because of the different specific ways in which they are introduced.
![]() at the terminal time
at the terminal time ![]() gives us an approximation of the terminal point
gives us an approximation of the terminal point ![]() of the perturbed trajectory. Namely, from (4.16) evaluated
at
of the perturbed trajectory. Namely, from (4.16) evaluated
at ![]() we have
we have