4.2.1 From Lagrange to Mayer form

As in Section 3.3.2, we define an additional state variable, $x^0\in\mathbb{R}$ , to be the solution of

$$\dot x^0=L(x,u),\qquad x^0(t_0)=0$$

and arrive at the augmented system

$$\begin{split}\dot x^0&=L(x,u)\\ \dot x&=f(x,u) \end{split}$$ (4.5)

with the initial condition $\Big({\textstyle{0}\atop \textstyle{x_0}}\Big)$ . The cost can then be rewritten as

$$J(u)=\int_{t_0}^{t_f}\dot x^0(t) dt=x^0(t_f)$$ (4.6)

which means that in the new coordinates the problem is in the Mayer form (there is a terminal cost and no running cost). Also, the target set becomes $[t_0,\infty)\times \mathbb{R}\times\{x_1\}=: [t_0,\infty)\times S'$ ; here $S'$ is the line in $\mathbb{R}^{n+1}$ that passes through $\Big({\textstyle{0}\atop \textstyle{x_1}}\Big)$ and is parallel to the $x^0$ -axis. To simplify the notation, we define

$$y:=\begin{pmatrix}x^0\\ x\end{pmatrix}\in\mathbb{R}^{n+1}$$

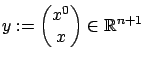
and write the system (4.5) more compactly as

$$\dot y=\begin{pmatrix}L(x,u) \\ f(x,u) \end{pmatrix}=:g(y,u)$$ (4.7)

(the right-hand side actually does not depend on $x^0$ ). Note that this system is well posed because we assumed that $L$ has the same regularity properties as $f$ .

An optimal trajectory $x^*(\cdot)$ of the original system in $\mathbb{R}^n$ corresponds in an obvious way to an optimal trajectory $y^*(\cdot)$ of the augmented system in $\mathbb{R}^{n+1}$ . The first component $x^{0,*}$ of $y^*$ describes the evolution of the cost in the original problem, and $x^*$ is recovered from $y^*$ by projection onto $\mathbb{R}^n$ parallel to the $x^0$ -axis. This situation is depicted in Figure 4.1 (note that $L$ is not necessarily positive, so $x^0$ need not actually be increasing along $y^*$ ). In this and all subsequent figures, the $x^0$ -axis will be vertical.

Figure: The optimal trajectory of the augmented system

From now on, we let $t^*$ denote the terminal time of the optimal trajectory $x^*$ (or, what is the same, of $y^*$ ). The next exercise offers a geometric interpretation of optimality; it will not be directly used in the current proof, but we will see a related idea in Section 4.2.6.

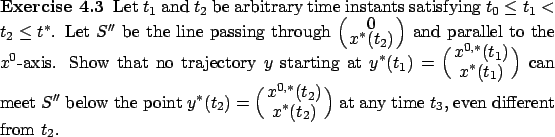
In the particular case when $t_2=t^*$ , the claim in the exercise should be obvious: no other trajectory starting from some point $y^*(t_1)$ on the optimal trajectory can hit the line $S'$ at a point lower than $y^*(t^*)$ . In other words, a final portion of the optimal trajectory must itself be optimal with respect to its starting point as the initial condition. This idea, known as the principle of optimality, is illustrated in Figure 4.2. (The reader will notice that we are using different axes in different figures.)

Figure: Principle of optimality

Another simple observation, which will be useful later, is that the Hamiltonian (4.2) can be equivalently represented as the following inner product in $\mathbb{R}^{n+1}$ :

$$H(x,u,p,p_0)=\left\langle\begin{pmatrix}p_0 \\ p \end{pmatrix},\begin{pmatrix}L(x,u) \\ f(x,u) \end{pmatrix}\right\rangle.$$ (4.8)