




Next: 4.2.4 Variational equation
Up: 4.2 Proof of the
Previous: 4.2.2 Temporal control perturbation
Contents
Index
4.2.3 Spatial control perturbation
We now construct control perturbations known as
``needle" perturbations, or Pontryagin-McShane perturbations. As the first
name suggests, they will be represented by pulses of short duration; the reason for
the second name is
that perturbations
of this kind
were first used by McShane in calculus of variations
(see Section 3.1.2)
and later adopted by Pontryagin's school for the proof of the maximum principle.
Let 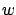 be an arbitrary element of
the control set
be an arbitrary element of
the control set 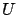 . Consider the interval
. Consider the interval
![$ I:=(b-\varepsilon a,
b]\subset (t_0,t^*)$](img1063.gif) , where
, where 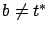 is a point of
continuity4.2 of
is a point of
continuity4.2 of 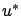 ,
, 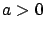 is arbitrary, and
is arbitrary, and
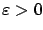 is
small. We
define the perturbed control
is
small. We
define the perturbed control
Figure 4.5 illustrates this control perturbation and the resulting
state trajectory perturbation. As the figure suggests, the perturbed trajectory  corresponding to
corresponding to 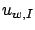 will deviate from
will deviate from 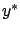 on the interval
on the interval 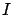 and
afterwards will ``run
parallel" to
and
afterwards will ``run
parallel" to 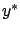 .
We now proceed to formally characterize the deviation over
.
We now proceed to formally characterize the deviation over 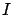 ; the behavior
of
; the behavior
of  over the interval
over the interval ![$ [b,t^*]$](img1070.gif) will be studied in Section 4.2.4.
will be studied in Section 4.2.4.
Figure:
A spatial control perturbation and its effect on the
trajectory
|
|
We will let 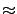 denote equality up to terms of order
denote equality up to terms of order
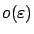 .
The first-order Taylor expansion of
.
The first-order Taylor expansion of 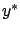 around
around 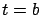 gives
gives
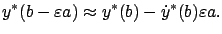 |
(4.10) |
Rearranging terms and using the fact that 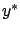 satisfies the differential equation (4.7) with
satisfies the differential equation (4.7) with 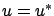 , we have
, we have
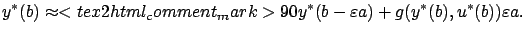 |
(4.11) |
On the other hand, the first-order Taylor expansion of the perturbed solution  around
around
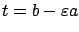 yields
yields
where by
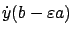 we mean the right-sided derivative of
we mean the right-sided derivative of  at
at
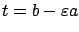 .
Since
.
Since
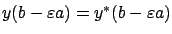 by
construction and
by
construction and  satisfies (4.7) with
satisfies (4.7) with 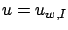 , we obtain
, we obtain
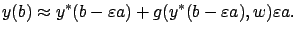 |
(4.12) |
We now apply the Taylor expansion to the last term in (4.12):
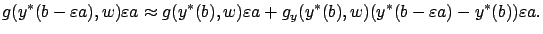 |
(4.13) |
In view of (4.10), the second term on the right-hand side of (4.13) is of order
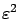 ; hence we can omit it and the approximation will remain valid.
Thus (4.12) simplifies to
; hence we can omit it and the approximation will remain valid.
Thus (4.12) simplifies to
Comparing this formula with (4.11), we arrive at
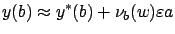 |
(4.14) |
where
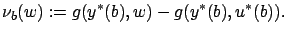 |
(4.15) |
Intuitively, this result makes sense: up to terms of order
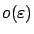 , the difference between the two states
, the difference between the two states 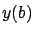 and
and 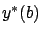 is the difference (4.15) between the state velocities at
is the difference (4.15) between the state velocities at 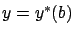 corresponding to
corresponding to 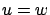 and
and 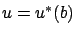 , multiplied by the length
, multiplied by the length
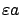 of the time interval on which the perturbation is acting.
of the time interval on which the perturbation is acting.





Next: 4.2.4 Variational equation
Up: 4.2 Proof of the
Previous: 4.2.2 Temporal control perturbation
Contents
Index
Daniel
2010-12-20
![]() be an arbitrary element of
the control set
be an arbitrary element of
the control set ![]() . Consider the interval
. Consider the interval
![]() , where
, where ![]() is a point of
continuity4.2 of
is a point of
continuity4.2 of ![]() ,
, ![]() is arbitrary, and
is arbitrary, and
![]() is
small. We
define the perturbed control
is
small. We
define the perturbed control
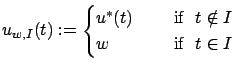
![]() denote equality up to terms of order
denote equality up to terms of order
![]() .
The first-order Taylor expansion of
.
The first-order Taylor expansion of ![]() around
around ![]() gives
gives