To continue our search for additional conditions (besides being an
extremal) which are necessary for a piecewise
![]() curve
curve ![]() to be a strong minimum, we now introduce a new concept. For a given Lagrangian
to be a strong minimum, we now introduce a new concept. For a given Lagrangian
![]() , the
Weierstrass excess function, or
, the
Weierstrass excess function, or ![]() -function, is defined
as
-function, is defined
as
The Weierstrass necessary condition for a strong minimum
states that if
![]() is a strong minimum, then
is a strong minimum, then
The Weierstrass necessary condition can be proved as follows.
Suppose that a curve ![]() is a strong minimum. Let
is a strong minimum. Let
![]() be a noncorner point of
be a noncorner point of ![]() , let
, let
![]() be such that the interval
be such that the interval
![]() contains no corner points of
contains no corner points of ![]() , and pick some
, and pick some
![]() . We construct a family of perturbed curves
. We construct a family of perturbed curves
![]() , parameterized by
, parameterized by
![]() , which are continuous, coincide with
, which are continuous, coincide with ![]() on the complement of
on the complement of
![]() , are linear with derivative
, are linear with derivative ![]() on
on
![]() , and differ from
, and differ from ![]() by a linear function on
by a linear function on
![]() . The precise definition is
. The precise definition is
It is clear that
Noting that the behavior of
![]() outside the interval
outside the interval
![]() does not depend on
does not depend on
![]() , we have
, we have
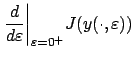 |
||
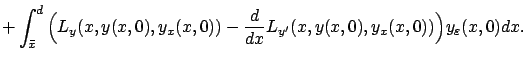 |
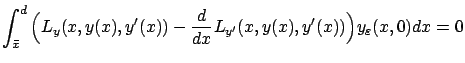
because
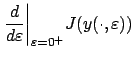 |
||
Weierstrass introduced the above necessary condition during his 1879 lectures on
calculus of variations. His original proof relied on an additional assumption
(normality) which was subsequently removed by McShane in 1939. Let us now
take a few moments to reflect on
the perturbation used in the proof we just gave. First, it is important to observe
that the perturbed curve
![]() is close to the original curve
is close to the original curve ![]() in the sense
of the 0-norm, but not necessarily in the sense of the 1-norm. Indeed,
it is clear that
in the sense
of the 0-norm, but not necessarily in the sense of the 1-norm. Indeed,
it is clear that
![]() as
as
![]() ; on the other hand,
the derivative of
; on the other hand,
the derivative of
![]() for
for ![]() immediately to the right of
immediately to the right of ![]() equals
equals ![]() , hence
, hence
![]() for all
for all
![]() ,
no matter how small. For this reason,
the necessary condition applies only to strong minima, unless we restrict
,
no matter how small. For this reason,
the necessary condition applies only to strong minima, unless we restrict
![]() to be sufficiently close to
to be sufficiently close to
![]() . Note also that the first variation
was not used in the proof. Thus we have already departed significantly from the
variational approach which we followed in Chapter 2. Derived
using a richer class of perturbations, the Weierstrass necessary condition
turns out to be powerful enough to yield as its corollaries
the Weierstrass-Erdmann corner
conditions from Section 3.1.1 as well as
Legendre's condition from Section 2.6.1.
. Note also that the first variation
was not used in the proof. Thus we have already departed significantly from the
variational approach which we followed in Chapter 2. Derived
using a richer class of perturbations, the Weierstrass necessary condition
turns out to be powerful enough to yield as its corollaries
the Weierstrass-Erdmann corner
conditions from Section 3.1.1 as well as
Legendre's condition from Section 2.6.1.
When solving this exercise, the reader should keep the following points in mind.
First, we know from Exercise 3.1
that the first Weierstrass-Erdmann corner condition is necessary
for weak extrema as well. This condition should thus follow directly from
the fact that ![]() is an extremal--i.e., satisfies the integral form (2.23) of the Euler-Lagrange equation--without the need
to apply the Weierstrass necessary condition. The second Weierstrass-Erdmann
corner condition,
on the other hand, is necessary only for strong extrema, and deducing
it requires
the full power of the Weierstrass necessary condition (including
a further analysis of what the latter implies for corner points). As for Legendre's condition,
it can be derived from the local version of the
Weierstrass necessary condition with
is an extremal--i.e., satisfies the integral form (2.23) of the Euler-Lagrange equation--without the need
to apply the Weierstrass necessary condition. The second Weierstrass-Erdmann
corner condition,
on the other hand, is necessary only for strong extrema, and deducing
it requires
the full power of the Weierstrass necessary condition (including
a further analysis of what the latter implies for corner points). As for Legendre's condition,
it can be derived from the local version of the
Weierstrass necessary condition with ![]() restricted to be close to
restricted to be close to ![]() for a given
for a given ![]() , thus confirming that
Legendre's condition is also necessary for weak extrema. Finally, when
, thus confirming that
Legendre's condition is also necessary for weak extrema. Finally, when ![]() is a
corner point, Legendre's
condition should read
is a
corner point, Legendre's
condition should read
![]()
The perturbation used in the above proof of the Weierstrass necessary condition is already quite close to the ones we will use later in the proof of the maximum principle. The main difference is that in the proof of the maximum principle, we will not insist on bringing the perturbed curve back to the original curve after the perturbation stops acting. Instead, we will analyze how the effect of a perturbation applied on a small interval propagates up to the terminal point.
There is a very insightful reformulation of the Weierstrass necessary condition which reveals its direct connection to the Hamiltonian maximization property discussed at the end of Section 2.6.1 (and thus to the maximum principle which we are steadily approaching). Let us write our Hamiltonian (2.63) as
Then a simple manipulation of (3.6) allows us to bring the
consistent with our earlier definition of the momentum (see Section 2.4.1). Therefore, the Weierstrass necessary condition simply says that if
Combining the Weierstrass necessary condition with the sufficient condition for a weak minimum from Section 2.6.2, one can obtain a sufficient condition for a strong minimum. The precise formulation of this condition requires a new concept (that of a field) and we will not develop it. While sufficient conditions for optimality are theoretically appealing, they tend to be less practical to apply compared to necessary conditions; we already saw this in Section 2.6.2 and will see again in Chapter 5.