| (4.51) |
Consider now a system with general linear time-invariant dynamics
Suppose that the control objective is to steer ![]() from a given
initial state
from a given
initial state ![]() to a given final state
to a given final state ![]() in minimal time.
To be sure that this problem is well posed, we assume that there
exists some control
in minimal time.
To be sure that this problem is well posed, we assume that there
exists some control ![]() that achieves the transfer from
that achieves the transfer from ![]() to
to
![]() (in some time). As we will see in
Section 4.5 (Theorem 4.3),
this guarantees that a time-optimal control
(in some time). As we will see in
Section 4.5 (Theorem 4.3),
this guarantees that a time-optimal control
![]() exists. We now
use the maximum principle to characterize it. The Hamiltonian is
exists. We now
use the maximum principle to characterize it. The Hamiltonian is
![]() . The Hamiltonian maximization condition implies
that
. The Hamiltonian maximization condition implies
that
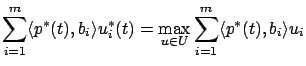
where
It has now become obvious that we must have
The adjoint equation is
![]() , which gives
, which gives
![]() . From this we obtain
. From this we obtain
![]() . This
is a real analytic function of
. This
is a real analytic function of ![]() ; hence, if it vanishes on some
time interval, then it vanishes for all
; hence, if it vanishes on some
time interval, then it vanishes for all ![]() , together with all its
derivatives. Calculating these derivatives at
, together with all its
derivatives. Calculating these derivatives at ![]() , we arrive
at the equalities
, we arrive
at the equalities
![[*]](crossref.gif) ). Therefore, to rule
out (4.55) it is enough to assume that
). Therefore, to rule
out (4.55) it is enough to assume that
Let us now collect the properties of the optimal control ![]() that we are able to derive under the above normality assumption.
None of the functions
that we are able to derive under the above normality assumption.
None of the functions
![]() equal 0 on any
time interval; being real analytic functions, they only have
finitely many zeros on the interval
equal 0 on any
time interval; being real analytic functions, they only have
finitely many zeros on the interval ![]() . Using the
formula (4.54), we see that each function
. Using the
formula (4.54), we see that each function ![]() only takes the values
only takes the values ![]() and switches between these values
finitely many times. Away from these switching times,
and switches between these values
finitely many times. Away from these switching times, ![]() is
uniquely determined by (4.54). We conclude that the
overall optimal control
is
uniquely determined by (4.54). We conclude that the
overall optimal control ![]() takes values only in the set of
vertices of the hypercube
takes values only in the set of
vertices of the hypercube ![]() , has finitely many
discontinuities (switches), and is unique everywhere else.
Generalizing the earlier notion, we say that controls taking
values in the set of vertices of
, has finitely many
discontinuities (switches), and is unique everywhere else.
Generalizing the earlier notion, we say that controls taking
values in the set of vertices of ![]() are bang-bang (or
have the bang-bang property); the result that we have just
obtained is a version of the bang-bang principle for
linear systems.
are bang-bang (or
have the bang-bang property); the result that we have just
obtained is a version of the bang-bang principle for
linear systems.
Before closing this discussion, it is instructive to see how the above bang-bang property can be established in a self-contained way, without relying on the maximum principle. More precisely, the argument outlined next essentially rederives the maximum principle from scratch for the particular problem at hand (in the spirit of Section 4.3.1). Solutions of the system (4.51) take the form
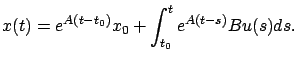
For
![$\displaystyle \int_{t_0}^{t^*} \langle p^*(t^*),e^{A(t^*- s) }Bu^*( s ) \rangle...
...le p^*(t^*),e^{A(t^*- s) }Bu( s )
\rangle d s \qquad \forall\,u:[t_0,t^*]\to U
$](img1400.gif)
which, in view of the formula
![$\displaystyle \int_{t_0}^{t^*} \langle p^*(s),Bu^*( s ) \rangle d
s\ge\int_{t_0}^{t^*} \langle p^*(s),Bu( s ) \rangle d s \qquad \forall\,u:[t_0,t^*]\to U.
$](img1402.gif)
From this it is not difficult to recover the fact that (4.53) must hold for (almost) all

The assumption of normality, which was needed to prove the
bang-bang property of time-optimal controls for ![]() a hypercube,
is quite strong.
A different, weaker
version of the bang-bang principle could be formulated as follows.
Rather than wishing for every time-optimal control to be
bang-bang, we could ask whether every state
a hypercube,
is quite strong.
A different, weaker
version of the bang-bang principle could be formulated as follows.
Rather than wishing for every time-optimal control to be
bang-bang, we could ask whether every state ![]() reachable from
reachable from
![]() by some control is also reachable from
by some control is also reachable from ![]() in the
same time by a bang-bang control; in other words, whether
reachable sets for bang-bang controls coincide with reachable sets
for all controls. This would imply that, even though not all
time-optimal controls are necessarily bang-bang, we can always
select one that is bang-bang. It turns out that this modified
bang-bang principle holds for every linear control system (no
controllability assumption is necessary) and every control set
in the
same time by a bang-bang control; in other words, whether
reachable sets for bang-bang controls coincide with reachable sets
for all controls. This would imply that, even though not all
time-optimal controls are necessarily bang-bang, we can always
select one that is bang-bang. It turns out that this modified
bang-bang principle holds for every linear control system (no
controllability assumption is necessary) and every control set
![]() that is a convex polyhedron. The proof requires a refinement
of the above argument and some additional
steps; see [Sus83, Section 8.1]
for details.
that is a convex polyhedron. The proof requires a refinement
of the above argument and some additional
steps; see [Sus83, Section 8.1]
for details.