



Next: 5.1.3 HJB equation
Up: 5.1 Dynamic programming and
Previous: 5.1.1 Motivation: the discrete
Contents
Index
5.1.2 Principle of optimality
We now return to the continuous-time optimal control problem that
we have been studying since Section 3.3, defined by the
control system (3.18) and the Bolza cost
functional (3.21). For concreteness, assume that we are
dealing with a fixed-time, free-endpoint problem, i.e., the target
set is
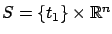 . (Handling other target sets requires
some modifications, on which we briefly comment in what follows.) We
can then write the cost functional as
. (Handling other target sets requires
some modifications, on which we briefly comment in what follows.) We
can then write the cost functional as
As we already remarked in Section 3.3.2, a more
accurate notation for this functional would be
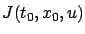 as
it depends on the initial data.
as
it depends on the initial data.
The basic idea of dynamic programming is to consider, instead of
the problem of minimizing
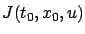 for given
for given 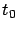 and
and
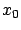 , the family of minimization problems associated
with the cost functionals
, the family of minimization problems associated
with the cost functionals
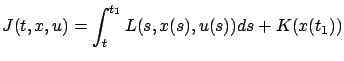 |
(5.1) |
where 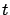 ranges over
ranges over 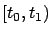 and
and 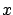 ranges over
ranges over
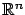 ; here
; here
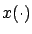 on the right-hand side denotes the state trajectory
corresponding to the control
on the right-hand side denotes the state trajectory
corresponding to the control 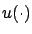 and satisfying
and satisfying 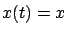 . (There is
a slight abuse of notation here; the second argument
. (There is
a slight abuse of notation here; the second argument 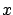 of
of 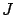 in (5.1) is a fixed point, and only the third argument
in (5.1) is a fixed point, and only the third argument 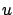 is a function of time.) In accordance with Bellman's
roadmap, our goal is to derive a dynamic relationship among
these problems, and ultimately to solve all of them.
is a function of time.) In accordance with Bellman's
roadmap, our goal is to derive a dynamic relationship among
these problems, and ultimately to solve all of them.
To this end, let us introduce the value function
![$\displaystyle V(t,x):=\inf_{u_{[t,t_1]}} J(t,x,u)$](img1562.gif) |
(5.2) |
where the notation
![$ u_{[t,t_1]}$](img1563.gif) indicates that the control
indicates that the control 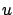 is
restricted to the interval
is
restricted to the interval ![$ [t,t_1]$](img1564.gif) . Loosely speaking, we can
think of
. Loosely speaking, we can
think of 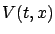 as the optimal cost (cost-to-go) from
as the optimal cost (cost-to-go) from
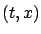 . It is important to note, however, that the existence of
an optimal control--and hence of the optimal cost--is not
actually assumed, which is why we work with an infimum rather than
a minimum in (5.2). If an optimal control exists, then
the infimum turns into a minimum and
. It is important to note, however, that the existence of
an optimal control--and hence of the optimal cost--is not
actually assumed, which is why we work with an infimum rather than
a minimum in (5.2). If an optimal control exists, then
the infimum turns into a minimum and 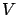 coincides with the
optimal cost-to-go. In general, the infimum need not be achieved,
and might even equal
coincides with the
optimal cost-to-go. In general, the infimum need not be achieved,
and might even equal 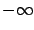 for some
for some 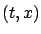 .
.
It is clear that the value function must satisfy the boundary
condition
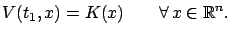 |
(5.3) |
In particular, if there is no terminal cost
(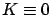 ) then we have
) then we have
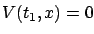 . The boundary
condition (5.3) is of course a consequence of our
specific problem formulation. If the problem involved a more
general target set
. The boundary
condition (5.3) is of course a consequence of our
specific problem formulation. If the problem involved a more
general target set
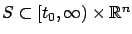 , then the boundary
condition would read
, then the boundary
condition would read
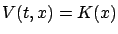 for
for
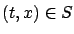 .
.
The basic principle of dynamic programming for the present case is
a continuous-time counterpart of the principle of optimality
formulated in Section 5.1.1, already familiar to us
from Chapter 4. Here we can state this property as
follows, calling it again the principle of optimality:
For every
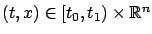 and every
and every
![$ {\scriptstyle\Delta}t\in(0,t_1-t]$](img1571.gif) , the value function
, the value function 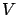 defined in (5.2) satisfies the relation
defined in (5.2) satisfies the relation
![$\displaystyle V(t,x)=\inf_{u_{[t,t+\Delta t]}}\left\{\int_t^{t+{\scriptstyle\De...
...( s,x(s),u(s))d s+V(t+{\scriptstyle\Delta}t,x(t+{\scriptstyle\Delta}t))\right\}$](img1572.gif) |
(5.4) |
where 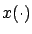 on the right-hand side is the state
trajectory corresponding to the control
on the right-hand side is the state
trajectory corresponding to the control
![$ u_{[t,t+{\scriptstyle\Delta}t]}$](img1573.gif) and
satisfying
and
satisfying 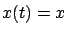 . The intuition behind this statement is that
to search for an optimal control, we can search over a small time
interval for a control that minimizes the cost over this interval
plus the subsequent optimal cost-to-go. Thus the minimization
problem on the interval
. The intuition behind this statement is that
to search for an optimal control, we can search over a small time
interval for a control that minimizes the cost over this interval
plus the subsequent optimal cost-to-go. Thus the minimization
problem on the interval ![$ [t,t_1]$](img1564.gif) is split into two, one on
is split into two, one on
![$ [t,t+{\scriptstyle\Delta}t]$](img1574.gif) and the other on
and the other on
![$ [t+{\scriptstyle\Delta}t,t_1]$](img1575.gif) ; see
Figure 5.3.
; see
Figure 5.3.
Figure:
Continuous time: principle of optimality
|
|
The above principle of optimality may seem obvious. However, it is
important to justify it rigorously, especially since we are using an
infimum and not assuming existence of optimal controls. We give
``one half" of the proof by verifying that
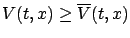 |
(5.5) |
where
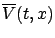 denotes the right-hand side
of (5.4):
denotes the right-hand side
of (5.4):
By (5.2) and the definition of infimum, for every
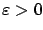 there exists a control
there exists a control
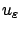 on
on ![$ [t,t_1]$](img1564.gif) such that
such that
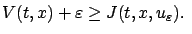 |
(5.6) |
Writing
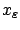 for the corresponding state trajectory, we have
for the corresponding state trajectory, we have
where the two inequalities follow directly from the definitions of
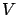 and
and
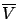 , respectively. Since (5.6) holds
with an arbitrary
, respectively. Since (5.6) holds
with an arbitrary
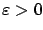 , the desired
inequality (5.5) is established.
, the desired
inequality (5.5) is established.




Next: 5.1.3 HJB equation
Up: 5.1 Dynamic programming and
Previous: 5.1.1 Motivation: the discrete
Contents
Index
Daniel
2010-12-20
![]() . (Handling other target sets requires
some modifications, on which we briefly comment in what follows.) We
can then write the cost functional as
. (Handling other target sets requires
some modifications, on which we briefly comment in what follows.) We
can then write the cost functional as
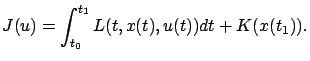
![]() for given
for given ![]() and
and
![]() , the family of minimization problems associated
with the cost functionals
, the family of minimization problems associated
with the cost functionals
![]() and every
and every
![]() , the value function
, the value function ![]() defined in (5.2) satisfies the relation
defined in (5.2) satisfies the relation
![$\displaystyle \overline V(t,x):=\inf_{u_{[t,t+\Delta t]}}\left\{\int_t^{t+{\scr...
...s,x(s),u(s))d s+V(t+{\scriptstyle\Delta}t,x(t+{\scriptstyle\Delta}t))\right\}.
$](img1579.gif)
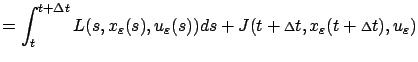
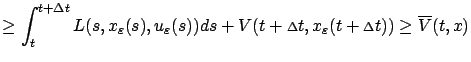
![]()