4.5 Existence of optimal controls

To motivate the subject of this section, let us consider the following (obviously absurd) claim: The largest positive integer is 1. To ``prove" this statement, let $N$ be the largest positive integer and suppose that $N\ne 1$ . Then we have $N^2>N$ , which contradicts the property of $N$ being the largest positive integer. Therefore, $N=1$ .

This argument is known as Perron's paradox. Although clearly farcical, it highlights a serious issue which we have been dodging up until now: it warns us about the danger of assuming the existence of an optimal solution. Indeed, finding the largest positive integer is an optimization problem. Of course, a solution to this problem does not exist. In the language of this book, the above reasoning correctly shows that $N=1$ is a necessary condition for optimality. Thus a necessary condition can be useless--even misleading--unless we know that a solution exists.

We know very well that the maximum principle only provides necessary conditions for optimality. The same is true for the Euler-Lagrange equation and several other results that we have derived along the way. We have said repeatedly that fulfillment of necessary conditions alone does not guarantee optimality. However, the basic question of whether an optimal solution even exists has not been systematically addressed yet, and it is time to do it now.

Suppose that we are given an optimal control problem which falls into the general class of problems formulated in Section 3.3. How can we ensure the existence of an optimal control? For a start, we must assume that there exists at least one control $u$ that drives the state of the system from the initial condition to the target set $S$ (more precisely, the pair $(t,x(t))$ should evolve from $(t_0,x_0)$ to $S$ ). Otherwise, the problem is ill posed (has infinite cost). We can view this as a type of controllability assumption. It may be nontrivial to check, especially for general control sets $U$ . Still, it would be nice if this controllability assumption were enough to guarantee the existence of an optimal control. Simple examples show that unfortunately this is not the case.

Observe that in the above example, arbitrarily fast transfer is possible because the control set $U=\mathbb{R}$ is unbounded. Let us see if the problem becomes well posed when $U$ is taken to be bounded.

This time, the difficulty is caused by the fact that the control set is not closed. The reader is probably beginning to guess that we want to have both boundedness and closedness, i.e., compactness. To make this statement precise, however, we should be working not with the control set $U$ itself but with the set of all points reachable from $x_0$ using controls that take values in $U$ . For $t\ge t_0$ , let us denote by $R^t(x_0)$ the set of points reachable from $x(t_0)=x_0$ at time $t$ (for a given control set $U$ ). We already worked with reachable sets on page , in the context of linear systems. We saw there that if $t^*-t_0$ is the fastest transfer time from $x_0$ to $x_1$ , then $x_1$ must be a boundary point of $R^{t^*}(x_0)$ ; this situation is illustrated in Figure 4.18.

Figure: Propagation of reachable sets $R^t(x_0)$ , $t_0\le t\le t^*$

In the two scalar examples considered earlier, the reachable set computation is straightforward and the negative conclusions are readily explained by the above property being impossible to satisfy. In Example 4.3, $R^t(x_0)=\mathbb{R}$ for all $t>0$ , which is unbounded and cannot contain $x_1=1$ on its boundary. In Example 4.4, $R^1(x_0)=[0,1)$ which is not closed and does not include the boundary point $1$ , while for each $t>1$ the set $R^t(x_0)$ already contains $1$ in its interior. We can now formulate a refined guess saying that for optimal controls to exist, we want to have compact reachable sets. We could generalize this discussion to target sets instead of fixed terminal points; we will also see that compactness of reachable sets is relevant not only for time-optimal control problems.

For nonlinear systems, explicit computation of reachable sets is usually not feasible. Instead, we can rely on the following general result known as Filippov's theorem: Given a control system in the standard form (3.18) with $u\in U$ , assume that its solutions exist on a time interval $[t_0,t_f]$ for all controls $u(\cdot)$ and that for every pair $(t,x)$ the set $\{f(t,x,u):u\in U\}$ is compact and convex. Then the reachable set $R^t(x_0)$ is compact for each $t\in[t_0,t_f]$ .

We do not prove this theorem but make some comments on it. For the result to be valid, controls must a priori be understood as measurable functions from $[t_0,t_f]$ to $U$ ; see the discussion on page . (We can hope to show afterwards that optimal controls belong to a nicer class of functions, e.g., that they enjoy the bang-bang property.) It is important to note that the first hypothesis in the theorem (existence of solutions on a given interval) is not implied by the second hypothesis (compactness and convexity of the right-hand side); for example, solutions of $\dot x=x^2+u$ blow up in finite time even for $U=\{0\}$ . Filippov's theorem actually has a stronger statement, from which compactness of $R^t(x_0)$ follows: it says that the set of all trajectories of the system, as a subset of $\mathcal C^0([t_0,t_f],\mathbb{R}^n)$ , is compact with respect to the topology induced by the 0-norm $\Vert\cdot\Vert _0$ , i.e., the topology of uniform convergence. Boundedness of the reachable sets can be shown without the convexity assumption, but convexity is crucial for establishing closedness (the argument relies on the separating hyperplane theorem). The next exercise should help clarify the role of the convexity assumption.

Filippov's theorem applies to useful classes of systems, most notably, to systems affine in controls given by (4.59) with compact and convex control sets $U$ . For such systems, the set $\{f(x)+G(x)u:u\in U\}$ is compact and convex for each $x$ as the image of $U$ under an affine map. As we already warned the reader, existence of solutions on a time interval of interest needs to be assumed separately. In the special case of linear systems (4.51), though, global existence of solutions is automatic. The right-hand side of the system is allowed to depend on time as well. For linear systems the reachable set $R^t(x_0)$ is also convex, as can be easily seen from convexity of $U$ and the variation-of-constants formula for solutions.

Filippov's theorem provides sufficient conditions for compactness of reachable sets. Earlier, we argued that compactness of reachable sets should be useful for proving existence of optimal controls. Let us now confirm that this is indeed true, at least for certain classes of problems. The connection between compactness of reachable sets and existence of optimal controls is especially easy to see for problems in the Mayer form (terminal cost only). Suppose that the control system satisfies the hypotheses of Filippov's theorem, that the cost is $J(u)=K(x_f)$ with $K$ a continuous function, and--in order to arrive at the simplest case--that the target set is $S= \{t_1\}\times\mathbb{R}^n$ (a fixed-time, free-endpoint problem). Since $K$ is a continuous function and $R^{t_1}(x_0)$ is a compact set, the Weierstrass Theorem (see page ) guarantees that $K$ has a global minimum over $R^{t_1}(x_0)$ . By the definition of $R^{t_1}(x_0)$ , there exists at least one control that steers the state to this minimum at time $t_1$ , and every such control is optimal.

For certain fixed-time problems in the Bolza form, it is possible to establish existence of optimal controls by combining compactness of the set of system trajectories (provided by the stronger form of Filippov's theorem) with continuity of the cost functional on this set and invoking the infinite-dimensional version of the Weierstrass Theorem (see page ). Alternatively, one can reduce the problem to the Mayer form (as in Section 3.3.2) and then use the previous result. In general, the argument needs to be tailored to a particular type of problem at hand. We will now show in detail how existence of optimal controls can be proved for linear time-optimal control problems, based on compactness--actually, just closedness--of reachable sets. The next result says that compactness and convexity of $U$ and a controllability assumption (the existence of some control achieving the desired transfer) is all we need for an optimal control to exist. (As we know from Section 4.4.2, such an optimal control is automatically bang-bang if $U$ is a hypercube, or can be chosen to be bang-bang if $U$ is an arbitrary convex polyhedron.)

PROOF. Let $t^*:=\inf \{t\ge t_0:x_1\in R^t(x_0)\}$ . The time $t^*$ is well defined because by the theorem's hypothesis the set over which the infimum is being taken is nonempty. (We note that, in view of boundedness of $U$ , we have $t^*>t_0$ unless $x_1=x_0$ .) We will be done if we show that $x_1\in R^{t^*}(x_0)$ , i.e., that $t^*$ is actually a minimum.^4.6 This will mean that there exists a control $u^*$ that transfers $x_0$ to $x_1$ at time $t^*$ , and by the definition of $t^*$ no control does it faster.

By the definition of infimum, there exists a sequence $t_k\searrow t^*$ such that $x_1\in R^{t_k}(x_0)$ for each $k$ . Then, by the definition of $R^{t_k}(x_0)$ , for each $k$ there is a control $u_k$ such that

$$x_1=e^{A(t_k-t_0)}x_0+\int_{t_0}^{t_k}e^{A(t_k-s)}Bu_k(s)ds.$$

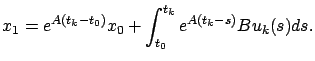
The above equation shows that the same point $x_1$ belongs to the reachable sets $R^{t_k}(x_0)$ for different $k$ . To be able to use the closedness property of reachable sets (guaranteed by Filippov's theorem), we would rather work with different points belonging to the same reachable set. To this end, let us truncate the trajectories corresponding to the controls $u_k$ at time $t^*$ and define, for each $k$ ,

$$x^k:=e^{A(t^*-t_0)}x_0+\int_{t_0}^{t^*}e^{A(t^*-s)}Bu_k(s)ds.$$ (4.68)

All these points by construction belong to the same reachable set $R^{t^*}(x_0)$ .

We now claim that the sequence of points $x^k$ converges to $x_1$ . If we establish this fact then the proof will be finished, because the closedness of the reachable set $R^{t^*}(x_0)$ will imply that $x_1\in R^{t^*}(x_0)$ as needed. To prove the convergence claim, let us write

$$x_1-x^k =\big(e^{A(t_k-t^*)}-I\big)e^{A(t^*-t_0)}x_0+\left( e^{A(t_k-t^*)... ...ht)\int_{t_0}^{t^*}e^{A(t^*-s)}Bu_k(s)ds+\int_{t^*}^{t_k}e^{A(t_k-s)} Bu_k(s)ds$$

$$=\left(e^{A\varepsilon _k}-I\right)x^k+\int_0^{\varepsilon _k}e^{A(\varepsilon _k-\tau)} Bu_k(t^*+\tau)d\tau$$

where we defined $\varepsilon _k:=t_k-t^*$ and made the substitution $s=t^*+\tau$ . Taking the norm on both sides, we have

$$\vert x_1-x^k\vert\le \big\Vert e^{A\varepsilon _k}-I\big\Vert\ve... ...max\big\{\vert e^{A\delta }Bu\vert:\delta \in[0,\varepsilon _k],\,u\in U\big\}.$$ (4.69)

Similarly, we can take the norm on both sides of (4.69) to obtain the bound

$$\vert x^k\vert\le\big\Vert e^{A(t^*-t_0)}\big\Vert \vert x_0\vert... ...-t_0)\max\big\{ \vert e^{A\delta }Bu\vert:\delta \in[0,t^*-t_0],\,u\in U\big\}$$

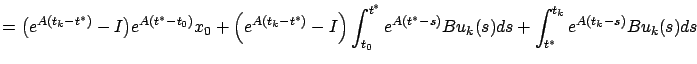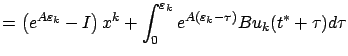which is independent of $k$ , implying that the sequence $\vert x^k\vert$ is uniformly bounded. Using this fact in (4.70) and noting that $\varepsilon _k\to 0$ hence also $\Vert e^{A\varepsilon _k}-I\Vert\to 0$ , we conclude that $\vert x_1-x^k\vert$ converges to 0 as claimed. 

Existence results are also available for other, more general classes of control problems (see Section 4.6 for further information). Although the proofs of such results are usually not constructive, the knowledge that a solution exists rules out the risks suggested by Perron's paradox and provides a basis for applying the maximum principle--which, as we have seen, often allows one to actually find an optimal control.