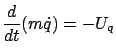 |
(2.39) |
Newton's second law of motion in the three-dimensional space can be written as the vector equation
It turns out that there
is a direct relationship between (2.40) and the Euler-Lagrange
equation. This is difficult to see right now
because the notation in (2.40)
is very different from the one we have been using. So, let us modify our
earlier notation to better match (2.40). First, let us write ![]() instead
of
instead
of ![]() for the independent variable. Second, let us write
for the independent variable. Second, let us write ![]() instead of
instead of ![]() for the dependent variable. Then also
for the dependent variable. Then also ![]() becomes
becomes ![]() and we have
and we have
![]() . In the new notation, the Euler-Lagrange equation becomes
. In the new notation, the Euler-Lagrange equation becomes
Some remarks on the above change of notation
are in order (as it is also a preview of things to come).The change from ![]() to
to ![]() is conceptually significant, because
it implies that the curves are parameterized by time and thus describe
some dynamic behavior (e.g.,
trajectories of a moving object). In problems such as Dido's problem or catenary
problem, where there is no motion with respect to time, this notation would
not be justified.
Other variational problems, such as the brachistochrone problem, do indeed
deal with paths of a moving particle. (We did not, however, explicitly
use time when formulating the brachistochrone problem, and
it would not make sense to just relabel
is conceptually significant, because
it implies that the curves are parameterized by time and thus describe
some dynamic behavior (e.g.,
trajectories of a moving object). In problems such as Dido's problem or catenary
problem, where there is no motion with respect to time, this notation would
not be justified.
Other variational problems, such as the brachistochrone problem, do indeed
deal with paths of a moving particle. (We did not, however, explicitly
use time when formulating the brachistochrone problem, and
it would not make sense to just relabel ![]() as
as
![]() in our earlier formulation of that problem.
Instead,
we would need to reparameterize the
in our earlier formulation of that problem.
Instead,
we would need to reparameterize the ![]() -trajectories with respect to time,
which yields a different Lagrangian; we will do this
in Section 3.2.)
In mechanics, as well as in control theory, time is
the default independent variable. Accordingly,
when we come to the optimal control part of the book, we will
make this change of notation permanent. For now, we adopt it just temporarily
while we discuss applications of calculus of variations in mechanics. As
for the (time-)dependent
coordinate variables, it is natural
to denote them by
-trajectories with respect to time,
which yields a different Lagrangian; we will do this
in Section 3.2.)
In mechanics, as well as in control theory, time is
the default independent variable. Accordingly,
when we come to the optimal control part of the book, we will
make this change of notation permanent. For now, we adopt it just temporarily
while we discuss applications of calculus of variations in mechanics. As
for the (time-)dependent
coordinate variables, it is natural
to denote them by ![]() and
and ![]() for planar curves
and by
for planar curves
and by ![]() ,
, ![]() and
and ![]() for spatial curves. In
general, the choice of a label
for the coordinate vector
is just a matter of preference and convention; the mechanics
literature typically favors
for spatial curves. In
general, the choice of a label
for the coordinate vector
is just a matter of preference and convention; the mechanics
literature typically favors ![]() or
or ![]() , while
in control theory it is customary to use
, while
in control theory it is customary to use ![]() .
.
Let us now compare (2.41) with (2.40). Is
there a choice of the Lagrangian ![]() that would make these two equations
the same? The answer is yes, and the reader will have no difficulty in
seeing that the following Lagrangian does the job:
that would make these two equations
the same? The answer is yes, and the reader will have no difficulty in
seeing that the following Lagrangian does the job:
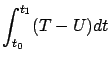
which is called the action integral. In general, these extremals are not necessarily minima. However, they are indeed minima--hence the term ``least action" is accurate--if the time horizon is sufficiently short; this will follow from the second-order sufficient condition for optimality, to be derived in Section 2.6.2.
For example, if the potential is 0, then
the trajectories are the extremals of
![]() ,
which are straight lines. We saw in
Example 2.2 that straight lines arise
as extremals when the Lagrangian is the arclength;
the kinetic energy gives the same extremals.
In the presence of gravity, the paths along which the action integral is
minimized can be viewed as ``straight lines" (shortest paths, or geodesics)
in a curved space whose metric is determined by gravitational forces.
This view of mechanics forms the basis
for Einstein's theory of general relativity.
,
which are straight lines. We saw in
Example 2.2 that straight lines arise
as extremals when the Lagrangian is the arclength;
the kinetic energy gives the same extremals.
In the presence of gravity, the paths along which the action integral is
minimized can be viewed as ``straight lines" (shortest paths, or geodesics)
in a curved space whose metric is determined by gravitational forces.
This view of mechanics forms the basis
for Einstein's theory of general relativity.
Observe the difference between the law that the derivative of
the momentum equals the force and the
principle that the action integral is
minimized. The former condition holds pointwise in time, while
the latter is a statement about the entire trajectory. However, their
relation is not surprising, because if the action integral is minimized then
every small piece of the trajectory must also deliver minimal action. In the
limit as the length of the piece approaches 0, we recover the differential
statement. We already discussed this
point in the general context of the Euler-Lagrange
equation (see page ![[*]](crossref.gif) ).
).
Now, what is the physical meaning of the Hamiltonian?
Substituting ![]() for
for ![]() in (2.28)-(2.29)
and using (2.42), we have
in (2.28)-(2.29)
and using (2.42), we have
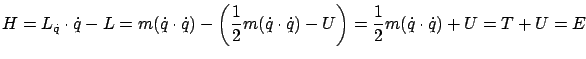
which is the total energy (kinetic plus potential). We see that the Hamiltonian not only enables a convenient rewriting of the Euler-Lagrange equation in the form of the canonical equations (2.30), but also has a very clear mechanical interpretation.
![]()
Recall that in Section 2.3.4 we studied two special cases for which we found conserved quantities, i.e., functions that remain constant along extremals. We now revisit these two conservation laws--as well as another related case--in the context of the principle of least action, which permits us to see their physical meaning.
CONSERVATION OF ENERGY. In a conservative system, the potential
is fixed and does not change with time. Since the kinetic
energy does not explicitly
depend on time either, we have
![]() . In other words, the
Lagrangian is invariant under time shifting.
In our old notation, this corresponds to the
``no
. In other words, the
Lagrangian is invariant under time shifting.
In our old notation, this corresponds to the
``no ![]() " case from Section 2.3.4, and we know that in
this case the Hamiltonian is conserved. We also just saw that the Hamiltonian
is the total energy of the system. Therefore, this is nothing but the well-known
principle of conservation of energy.
" case from Section 2.3.4, and we know that in
this case the Hamiltonian is conserved. We also just saw that the Hamiltonian
is the total energy of the system. Therefore, this is nothing but the well-known
principle of conservation of energy.
CONSERVATION OF MOMENTUM. Suppose that no force
is acting on the system (i.e., the system is closed). Since the force
is given by
![]() , this implies that
, this implies that ![]() must be constant. The kinetic
energy
must be constant. The kinetic
energy ![]() depends on
depends on ![]() but not on
but not on ![]() . Thus the Lagrangian
. Thus the Lagrangian
![]() does not
explicitly depend on
does not
explicitly depend on ![]() , which means that it is invariant
under
parallel translations.
This situation corresponds to the
``no
, which means that it is invariant
under
parallel translations.
This situation corresponds to the
``no ![]() " case from Section 2.3.4,
where we saw that the momentum,
" case from Section 2.3.4,
where we saw that the momentum,
![]() in the present
notation,
is conserved. A more general statement is that for
each coordinate
in the present
notation,
is conserved. A more general statement is that for
each coordinate ![]() that does not appear in
that does not appear in ![]() , the
corresponding component
, the
corresponding component
![]() of the momentum is conserved.
of the momentum is conserved.
CONSERVATION OF ANGULAR MOMENTUM.
Consider a planar motion in a central field; in polar coordinates
![]() , this is defined by the property that
, this is defined by the property that
![]() , i.e., the potential depends only on the radius and not on the
angle. This means that
no torque is acting on the system, making the Lagrangian
, i.e., the potential depends only on the radius and not on the
angle. This means that
no torque is acting on the system, making the Lagrangian ![]() invariant under
rotations. Now we can use the fact
(noted at the end of Section 2.3.3)
that the Euler-Lagrange equation looks the same in all coordinate systems. In particular,
in polar coordinates we have
invariant under
rotations. Now we can use the fact
(noted at the end of Section 2.3.3)
that the Euler-Lagrange equation looks the same in all coordinate systems. In particular,
in polar coordinates we have
These are familiar expressions for the angular momentum.
We remark that all of the above examples are special instances of a general result known as Noether's theorem, which says that invariance of the action integral under some transformation (e.g., time shift, translation, rotation) implies the existence of a conserved quantity.