We are now interested in obtaining a second-order
sufficient condition for proving optimality of a given test curve ![]() . Looking at the
expansion (2.56) and recalling our earlier discussions, we know
that we want to have
. Looking at the
expansion (2.56) and recalling our earlier discussions, we know
that we want to have
![]() for all admissible
perturbations, which means having a
strict inequality in (2.61). In addition, we need
some uniformity to be able
to dominate the
for all admissible
perturbations, which means having a
strict inequality in (2.61). In addition, we need
some uniformity to be able
to dominate the
![]() term.
Since we saw that the
term.
Since we saw that the ![]() -dependent term inside the integral
in (2.61) is the dominant term in the second variation,
it is natural to conjecture--as Legendre did--that having
-dependent term inside the integral
in (2.61) is the dominant term in the second variation,
it is natural to conjecture--as Legendre did--that having
![]() for all
for all ![]() should be sufficient for the second variation to be positive definite.
Legendre tried to prove this implication using the following
clever approach. For every differentiable function
should be sufficient for the second variation to be positive definite.
Legendre tried to prove this implication using the following
clever approach. For every differentiable function
![]() we have
we have
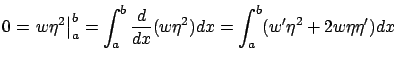
where the first equality follows from the constraint
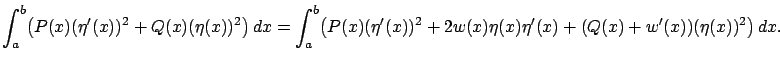
Now, the idea is to find a function
Let us suppose that we found a function ![]() satisfying (2.64).
Then our second variation can be written as
satisfying (2.64).
Then our second variation can be written as
The problem with the foregoing reasoning is that the
Riccati differential equation (2.64) may have a finite escape time, i.e., the solution ![]() may not exist on the whole interval
may not exist on the whole interval ![]() .
For example, if
.
For example, if ![]() and
and
![]() then (2.64) becomes
then (2.64) becomes
![]() . Its solution
. Its solution
![]() , where
the constant
, where
the constant ![]() depends on the choice of the initial condition, blows up when
depends on the choice of the initial condition, blows up when
![]() is an odd integer multiple of
is an odd integer multiple of ![]() . This means that
. This means that ![]() will not exist
on all of
will not exist
on all of ![]() for any choice of
for any choice of ![]() if
if
![]() .
.
We see that a sufficient condition for optimality
should involve, in addition to an inequality like
![]() holding pointwise along the curve, some ``global" considerations
applied to the entire curve.
In fact, this becomes intuitively clear if we observe
that a concatenation of optimal
curves is not necessarily optimal. For example, consider the
two great-circle arcs on a sphere shown in Figure 2.13. Each arc
minimizes the distance between its endpoints, but this statement is no longer
true for their concatenation--even when compared with
nearby curves. At the same time,
the concatenated arc would still satisfy
any pointwise condition fulfilled by the two pieces.
holding pointwise along the curve, some ``global" considerations
applied to the entire curve.
In fact, this becomes intuitively clear if we observe
that a concatenation of optimal
curves is not necessarily optimal. For example, consider the
two great-circle arcs on a sphere shown in Figure 2.13. Each arc
minimizes the distance between its endpoints, but this statement is no longer
true for their concatenation--even when compared with
nearby curves. At the same time,
the concatenated arc would still satisfy
any pointwise condition fulfilled by the two pieces.
So, we need to ensure the existence of a solution for the
differential equation (2.64) on the whole interval ![]() .
This issue, which escaped Legendre's attention, was pointed out by
Lagrange in 1797.
However, it was only in 1837, after 50 years had passed since Legendre's
investigation, that Jacobi closed the gap by
providing a missing ingredient which we now describe.
The first step is to reduce the quadratic first-order
differential equation (2.64)
to another differential equation, linear but of second
order, by
making the substitution
.
This issue, which escaped Legendre's attention, was pointed out by
Lagrange in 1797.
However, it was only in 1837, after 50 years had passed since Legendre's
investigation, that Jacobi closed the gap by
providing a missing ingredient which we now describe.
The first step is to reduce the quadratic first-order
differential equation (2.64)
to another differential equation, linear but of second
order, by
making the substitution
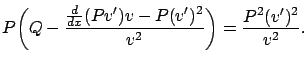
Multiplying both sides of this equation by
Since (2.67) is a second-order differential equation, the initial
data at ![]() needed to uniquely
specify a solution consists of
needed to uniquely
specify a solution consists of ![]() and
and ![]() . In addition, note that if
. In addition, note that if ![]() is a solution
of (2.67) then
is a solution
of (2.67) then ![]() is also a solution for every constant
is also a solution for every constant
![]() . By adjusting
. By adjusting ![]() appropriately, we can thus assume with no loss
of generality that
appropriately, we can thus assume with no loss
of generality that ![]() (since we are not interested
in
(since we are not interested
in ![]() being identically 0). Among such solutions, let us consider the one
that starts at 0, i.e., set
being identically 0). Among such solutions, let us consider the one
that starts at 0, i.e., set ![]() . A point
. A point ![]() is said to be conjugate
to
is said to be conjugate
to ![]() if this solution
if this solution ![]() hits 0 again at
hits 0 again at ![]() , i.e.,
, i.e.,
![]() (see Figure 2.14).
It is clear that conjugate points are completely determined by
(see Figure 2.14).
It is clear that conjugate points are completely determined by ![]() and
and ![]() ,
which in turn depend, through (2.59),
only on the test curve
,
which in turn depend, through (2.59),
only on the test curve ![]() and the Lagrangian
and the Lagrangian ![]() in the
original variational problem.
in the
original variational problem.
Conjugate points have a number of interesting properties and
interpretations, and their
theory is outside the scope of this book. We do mention the following
interesting
fact, which involves a concept that we will see again later when proving
the maximum principle. If we consider two neighboring extremals (solutions of the
Euler-Lagrange equation) starting from the same point at ![]() , and if
, and if ![]() is a point
conjugate to
is a point
conjugate to ![]() , then at
, then at ![]() the distance between these two extremals
becomes small (an infinitesimal of higher order) relative to the distance between the two extremals as well as between their derivatives over
the distance between these two extremals
becomes small (an infinitesimal of higher order) relative to the distance between the two extremals as well as between their derivatives over ![]() .
As their distance over
.
As their distance over ![]() approaches 0, the two extremals
actually intersect at a point whose
approaches 0, the two extremals
actually intersect at a point whose ![]() -coordinate approaches
-coordinate approaches ![]() . The reason behind
this phenomenon is that
the Jacobi equation is, approximately, the differential equation satisfied
by the difference between two neighboring extremals; the next exercise makes this
statement
precise.
. The reason behind
this phenomenon is that
the Jacobi equation is, approximately, the differential equation satisfied
by the difference between two neighboring extremals; the next exercise makes this
statement
precise.
We see from (2.68) that ![]() , which is
the difference between the two extremals,
satisfies the Jacobi equation (2.67) modulo terms of higher order.
A linear differential equation that describes,
within terms of higher order, the propagation
of the difference between two nearby solutions
of a given differential equation is called the variational equation
(corresponding to the given differential equation). In
this sense, the Jacobi equation is the variational equation for the Euler-Lagrange equation.
This property
can be shown to imply the claims we made before the exercise.
Intuitively speaking,
a conjugate point is where different neighboring extremals
starting from the same point meet again (approximately). If we revisit
the example of shortest-distance curves on a sphere, we see that conjugate points
correspond to diametrically
opposite points: all extremals
(which are great-circle arcs)
with a given initial point intersect after completing half a circle.
We will encounter the concept of a variational equation again in Section 4.2.4.
, which is
the difference between the two extremals,
satisfies the Jacobi equation (2.67) modulo terms of higher order.
A linear differential equation that describes,
within terms of higher order, the propagation
of the difference between two nearby solutions
of a given differential equation is called the variational equation
(corresponding to the given differential equation). In
this sense, the Jacobi equation is the variational equation for the Euler-Lagrange equation.
This property
can be shown to imply the claims we made before the exercise.
Intuitively speaking,
a conjugate point is where different neighboring extremals
starting from the same point meet again (approximately). If we revisit
the example of shortest-distance curves on a sphere, we see that conjugate points
correspond to diametrically
opposite points: all extremals
(which are great-circle arcs)
with a given initial point intersect after completing half a circle.
We will encounter the concept of a variational equation again in Section 4.2.4.
Now, suppose that the interval ![]() contains no points conjugate to
contains no points conjugate to ![]() .
Let us see how this may help us in our task of finding a solution
.
Let us see how this may help us in our task of finding a solution ![]() of the
Jacobi equation (2.67) that does not equal 0 anywhere on
of the
Jacobi equation (2.67) that does not equal 0 anywhere on ![]() .
The absence of conjugate points means, by definition, that the solution with the
initial
data
.
The absence of conjugate points means, by definition, that the solution with the
initial
data ![]() and
and ![]() never returns to 0 on
never returns to 0 on ![]() . This is not yet
a desired solution because we cannot have
. This is not yet
a desired solution because we cannot have ![]() .
What we can do, however, is make
.
What we can do, however, is make ![]() very small but positive. Using the property of continuity with respect to
initial conditions for solutions of differential equations, it is possible to
show that
such a solution will remain positive everywhere on
very small but positive. Using the property of continuity with respect to
initial conditions for solutions of differential equations, it is possible to
show that
such a solution will remain positive everywhere on ![]() .
.
In view of our earlier discussion, we conclude that the second variation
![]() is positive definite (on the space of admissible perturbations)
if
is positive definite (on the space of admissible perturbations)
if ![]() for all
for all ![]() and there are no points conjugate to
and there are no points conjugate to ![]() on
on ![]() .
We remark in passing that the absence of points conjugate to
.
We remark in passing that the absence of points conjugate to ![]() on
on
![]() is also a necessary condition for
is also a necessary condition for
![]() to be positive definite, and if
to be positive definite, and if
![]() is positive semidefinite then no interior point of
is positive semidefinite then no interior point of ![]() can be conjugate to
can be conjugate to ![]() .
We are now ready to state the following second-order sufficient condition
for optimality: An extremal
.
We are now ready to state the following second-order sufficient condition
for optimality: An extremal ![]() is a strict minimum if
is a strict minimum if
![]() for all
for all ![]() and the interval
and the interval
![]() contains no points conjugate to
contains no points conjugate to ![]() .
.
Note that we do not yet have a proof of this result.
Referring to the second-order expansion (2.56),
we know that under the conditions just listed
![]() (since
(since
![]() is an extremal) and
is an extremal) and
![]() given by (2.58)
is positive, but we still need to
show that
given by (2.58)
is positive, but we still need to
show that
![]() dominates the higher-order term
dominates the higher-order term
![]() which
has the properties established in Exercise 2.12.
Since
which
has the properties established in Exercise 2.12.
Since
![]() on
on ![]() ,
we can pick a small enough
,
we can pick a small enough
![]() such that
such that
![]() for all
for all ![]() . Consider the integral
. Consider the integral
In light of our earlier derivation of Legendre's condition, we know that the
term depending on ![]() is in some sense
the dominant term in (2.60),
and the inequality (2.70) indicates that we are in good shape.
Formally, we can handle the other,
is in some sense
the dominant term in (2.60),
and the inequality (2.70) indicates that we are in good shape.
Formally, we can handle the other, ![]() -dependent term in (2.60)
as follows.
Use the Cauchy-Schwarz inequality with respect to the
-dependent term in (2.60)
as follows.
Use the Cauchy-Schwarz inequality with respect to the
![]() norm2.4 to write
norm2.4 to write
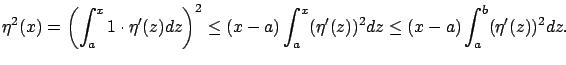
From this, we have
The above sufficient condition is not
as constructive and practical as the first-order and second-order
necessary conditions,
because to apply it one needs to study conjugate points.
The simpler necessary conditions can be exploited first, to see
if they help narrow down candidates for an optimal solution. It should be observed,
though, that the existence of conjugate points can be ruled out if the interval
![]() is taken to be sufficiently small.
is taken to be sufficiently small.
As for the multiple-degrees-of-freedom setting, let us make the simplifying assumption that ![]() is a symmetric matrix (i.e.,
is a symmetric matrix (i.e.,
![]() for all
for all
![]() ). Then it is not difficult to show, following steps similar to those that led us to (2.58), that the second variation
). Then it is not difficult to show, following steps similar to those that led us to (2.58), that the second variation
![]() is given
by the formula
is given
by the formula
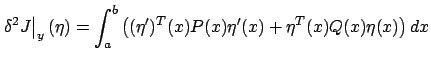
where
(note that