2.3.1 Euler-Lagrange equation

We continue to follow the notational convention of Chapter 1 and denote by ${L}_{x}$ , ${L}_{y}$ , ${L}_{z}$ , ${L}_{{x}{x}}$ , ${L}_{{x}{y}}$ , etc. the partial derivatives of the Lagrangian $L=L(x,y,z)$ . To keep things simple, we assume that all derivatives appearing in our calculations exist and are continuous. While we will not focus on spelling out the weakest possible regularity assumptions on $L$ , we will make some remarks to clarify this issue in Section 2.3.3.

Let $y=y(x)$ be a given test curve in $A$ . For a perturbation $\eta$ in (2.10) to be admissible, the new curve (2.10) must again satisfy the boundary conditions (2.8). Clearly, this is true if and only if

$$\eta(a)=\eta(b)=0.$$ (2.11)

In other words, we must only consider perturbations vanishing at the endpoints. Now, the first-order necessary condition (1.37) says that if $y$ is a local extremum of $J$ , then for every $\eta$ satisfying (2.11) we must have $\left.\delta J\right\vert _{y}(\eta)=0$ . (We denoted extrema by $y^*$ in (1.37) but here we drop the asterisks to avoid overly cluttered notation.) In the present case we want to go further and use the specific form of $J$ given by (2.9) to arrive at a more explicit condition in terms of the Lagrangian $L$ .

Recall that the first variation $\left.\delta J\right\vert _{y}$ was defined via

$$J(y+\alpha \eta)=J(y)+\left.\delta J\right\vert _{y} (\eta)\alpha+o(\alpha).$$ (2.12)

The left-hand side of (2.12) is

$$J(y+\alpha\eta)=\int_a^b L(x,y(x)+\alpha\eta(x),y'(x)+\alpha\eta'(x))dx.$$ (2.13)

We can write down its first-order Taylor expansion with respect to $\alpha$ by expanding the expression inside the integral with the help of the chain rule:

$$J(y+\alpha \eta)=\int_a^b \big(L(x,y(x),y'(x))+{L}_{ y}(x,y(x),y'(x))\alpha\eta(x)+{L}_{z}(x,y(x),y'(x))\alpha\eta'(x) +o(\alpha)\big)dx.$$

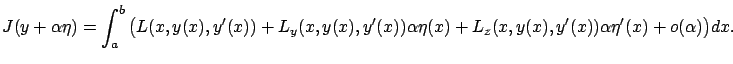
Matching this with the right-hand side of (2.12), we deduce that the first variation is

$$\left.\delta J\right\vert _{y}(\eta)=\int_a^b \big({L}_{ y}(x,y(x),y'(x))\eta(x)+{L}_{z}(x,y(x),y'(x))\eta'(x)\big)dx.$$ (2.14)

Note that, proceeding slightly differently, we could arrive at the same result by remembering from (1.34)-(1.36) that

$$\left.\delta J\right\vert _{y}(\eta)=\lim_{\alpha\to 0}\frac{J(y+... ...a)-J(y)}{\alpha}=\left.\frac d{d\alpha}\right\vert _{\alpha=0} J(y+\alpha\eta)$$

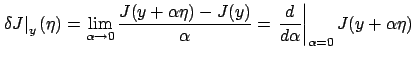
and using differentiation under the integral sign on the right-hand side of (2.13).

We see that the first variation depends not just on $\eta$ but also on $\eta'$ . This is not surprising since $L$ has $y'$ as one of its arguments. However, we can eliminate the dependence on $\eta'$ if we apply integration by parts to the second term on the right-hand side of (2.14):

$$\left.\delta J\right\vert _{y}(\eta)=\int_a^b\Big({L}_{y}(x,y(x),... ...,y(x),y'(x))\eta(x)\Big)dx+\left.{L}_{z}(x,y(x),y'(x))\eta(x)\right\vert _{a}^b$$ (2.15)

where the last term is 0 when $\eta$ satisfies the boundary conditions (2.11). Thus we conclude that if $y$ is an extremum, then we must have

$$\int_a^b\Big({L}_{y}(x,y(x),y'(x))-\frac d{dx}{L}_{z}(x,y(x),y'(x))\Big)\eta(x) dx=0$$ (2.16)

for all $\mathcal C^1$ curves $\eta$ vanishing at the endpoints $x=a$ and $x=b$ .

The condition (2.16) does not yet give us a practically useful test for optimality, because we would need to check it for all admissible perturbations $\eta$ . However, it is logical to suspect that the only way (2.16) can hold is if the term inside the parentheses--which does not depend on $\eta$ --equals 0 for all $x$ . The next lemma shows that this is indeed the case.

PROOF. Suppose that $\xi(\bar x)\ne 0$ for some $\bar x\in[a,b]$ . By continuity, $\xi$ is then nonzero and maintains the same sign on some subinterval $[c,d]$ containing $\bar x$ . Just for concreteness, let us say that $\xi$ is positive on $[c,d]$ .

Figure: The graph of $\eta$

Construct a function $\eta\in\mathcal C^1([a,b],\mathbb{R})$ that is positive on $(c,d)$ and 0 everywhere else (see Figure 2.7). For example, we can set $\eta(x)=(x-c)^2(x-d)^2$ for $x\in[c,d]$ and $\eta(x)=0$ otherwise. This gives $\int_a^b \xi(x)\eta(x) dx>0$ , and we reach a contradiction.

It follows from (2.16) and Lemma 2.1 that for $y(\cdot)$ to be an extremum, a necessary condition is

$${L}_{y}(x,y(x),y'(x))=\frac d{dx}{L}_{ z}(x,y(x),y'(x))\qquad\forall\,x\in[a,b].$$ (2.17)

This is the celebrated Euler-Lagrange equation providing the first-order necessary condition for optimality. It is often written in the shorter form

$$\fbox{${L}_{ y}=\dfrac d{dx}{L}_{ y'}$}$$ (2.18)

We must keep in mind, however, that the correct interpretation of the Euler-Lagrange equation is (2.17): $y$ and $y'$ are treated as independent variables when computing the partial derivatives ${L}_{y}$ and ${L}_{ y'}$ , then one plugs in for these variables the position $y(x)$ and velocity $y'(x)$ of the curve, and finally the differentiation with respect to $x$ is performed using the chain rule. Written out in detail, the right-hand side of (2.17) is

$$\frac d{dx}{L}_{z}(x,y(x),y'(x))={L}_{{ z}{ x}}(x,y(x),y'(x))+{L}_{{ z}{ y}}(x,y(x),y'(x))y'(x)+{L}_{{z}{z}}(x,y(x),y'(x))y''(x).$$ (2.19)

It might not be necessary to actually perform all of these operations, though; sometimes a shortcut is possible, as in the next example.

The functional $J$ to be minimized is given by the integral of the Lagrangian $L$ along a path, while the Euler-Lagrange equation involves derivatives of $L$ and must hold for every point on the optimal path; observe that the integral has disappeared. The underlying reason is that if a path is optimal, then every infinitesimally small portion of it is optimal as well (no ``shortcuts" are possible). The exact mechanism by which we pass from the statement that the integral is minimized to the pointwise condition is revealed by Lemma 2.1 and its proof.

Trajectories satisfying the Euler-Lagrange equation (2.18) are called extremals. Since the Euler-Lagrange equation is only a necessary condition for optimality, not every extremal is an extremum. We see from (2.19) that the equation (2.18) is a second-order differential equation; thus we expect that generically, the two boundary conditions (2.8) should be enough to specify a unique extremal. When this is true--as is the case in the above example--and when an optimal curve is known to exist, we can actually conclude that the unique extremal gives the optimal solution. In general, the question of existence of optimal solutions is not trivial, and the following example should serve as a warning. (We will come back to this issue later in the context of optimal control.)