2.3.3 Technical remarks

It is straightforward to extend the necessary condition (2.18) to the multiple-degrees-of-freedom setting, in which $y=(y_1,\dots,y_n)^T\in\mathbb{R}^n$ . The same derivation is valid, provided that ${L}_{y}$ and ${L}_{z}$ are interpreted as gradient vectors of $L$ with respect to $y$ and $z$ , respectively, and by products of vector quantities (such as ${L}_{y}\cdot \eta$ ) one means inner products in $\mathbb{R}^n$ . The result is the same Euler-Lagrange equation (2.18), which is now perhaps easier to apply and interpret if it is written componentwise:

$${L}_{ y_i}=\dfrac d{dx}{L}_{ y'_i},\qquad i=1,\dots,n.$$ (2.20)

Returning to the single-degree-of-freedom case, let us examine more carefully under what differentiability assumptions our derivation of the Euler-Lagrange equation is valid. We applied Lemma 2.1 to the function $\xi$ given by the expression inside the large parentheses in (2.16), whose second term is shown in more detail in (2.19). In the lemma, $\xi$ must be continuous. The appearance of second-order partial derivatives of $L$ in (2.19) suggests that we should assume $L\in\mathcal C^2$ . Somewhat more alarmingly, the presence of the term ${L}_{{z}{z}} y''$ indicates that we should assume $y\in \mathcal C^2$ , and not merely $y\in\mathcal C^1$ as in our original formulation of the Basic Calculus of Variations Problem. Fortunately, we can avoid making this assumption if we proceed more carefully, as follows. Let us apply integration by parts to the first term rather than the second term on the right-hand side of (2.14):

$$\left.\delta J\right\vert _{y}(\eta) =\int_a^b\Big(-\eta'(x)\int_a^x{L}_{y}(w,y(w),y'(w))dw +{L}_{ z}(x,y(x),y'(x))\eta'(x)\Big)dx$$

$$+ \left.\eta(x)\int_a^x{L}_{y}(w,y(w),y'(w))dw\right\vert _{a}^b$$

where the last term again vanishes for our class of perturbations $\eta$ . Thus an extremum $y$ must satisfy

$$\int_a^b\Big({L}_{z}(x,y(x),y'(x))-\int_a^x{L}_{y}(w,y(w),y'(w))dw \Big)\eta'(x) dx=0.$$ (2.21)

We now need the following modification of Lemma 2.1.

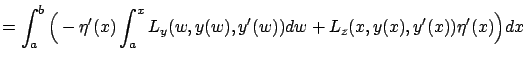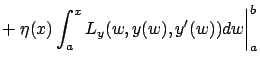From (2.22) and Lemma 2.2 we obtain that along an optimal curve we must have

$${L}_{z}(x,y(x),y'(x))=\int_a^x{L}_{y}(w,y(w),y'(w))dw+C$$ (2.22)

where $C$ is a constant. It follows that the derivative $\frac d{dx}{L}_{z}(x,y(x),y'(x))$ indeed exists and equals ${L}_{y}(x,y(x),y'(x))$ , and we do not need to make extra assumptions to guarantee the existence of this derivative. In other words, curves on which the first variation vanishes automatically enjoy additional regularity. Thus for the necessary condition described by the Euler-Lagrange equation to be valid, it is enough to assume that $y\in\mathcal C^1$ and $L\in \mathcal C^1$ . The integral form (2.23) of the Euler-Lagrange equation actually applies to extrema over piecewise $\mathcal C^1$ curves as well, although we would need a more general version of Lemma 2.2 to establish this fact.^2.2 The $\mathcal C^1$ assumption on $L$ can be further relaxed; note, in particular, that the partial derivative ${L}_{x}$ did not appear anywhere in our analysis.

It can be shown that the Euler-Lagrange equation is invariant under arbitrary changes of coordinates, i.e., it takes the same form in every coordinate system. This allows one to pick convenient coordinates when studying a specific problem. For example, in certain mechanical problems it is natural to use polar coordinates; we will come across such a case in Section 2.4.3.