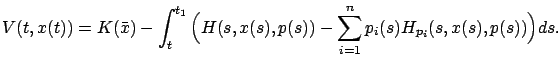Next: 7.3 Riccati equations and
Up: 7.2 HJB equation, canonical
Previous: 7.2.1 Method of characteristics
Contents
Index
7.2.2 Canonical equations as characteristics of the HJB
equation
We will now show that Hamilton's canonical equations arise as the characteristics--or, more precisely, characteristic strips--of the HJB equation. With some abuse of notation, let us write the
HJB equation as
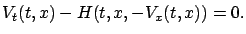 |
(7.15) |
Note that we did not include the control  as an argument in
as an argument in 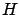 ; instead,
we assume that the control that maximizes the Hamiltonian has already been plugged in. (This formulation also covers the calculus of variations and mechanics settings, where the velocity variable is eliminated via the Legendre transformation.) We know that we can bring the PDE (7.15) to the form (7.9) by introducing the extra state variable
; instead,
we assume that the control that maximizes the Hamiltonian has already been plugged in. (This formulation also covers the calculus of variations and mechanics settings, where the velocity variable is eliminated via the Legendre transformation.) We know that we can bring the PDE (7.15) to the form (7.9) by introducing the extra state variable
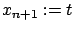 (cf. Section 5.3.3). We can thus write down the characteristic equations (7.14) for this particular PDE. Since the time
(cf. Section 5.3.3). We can thus write down the characteristic equations (7.14) for this particular PDE. Since the time 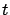 is present in (7.15), we can use it as the independent variable and write
is present in (7.15), we can use it as the independent variable and write 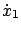 , etc. We also define the costates
, etc. We also define the costates
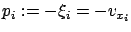 , which is consistent with our earlier convention (see Section 5.2). Then the equations (7.14) immediately yield
, which is consistent with our earlier convention (see Section 5.2). Then the equations (7.14) immediately yield
(plus one additional equation
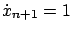 which is redundant) as well as
which is redundant) as well as
where we used the fact that 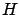 does not depend on
does not depend on 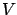 (hence the term
(hence the term 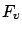 in (7.14) vanishes). Thus we have indeed recovered the familiar canonical differential equations.
in (7.14) vanishes). Thus we have indeed recovered the familiar canonical differential equations.
Finally, there is one more equation in (7.14) which describes the evolution of 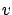 . Here it tells us that the value function satisfies
. Here it tells us that the value function satisfies
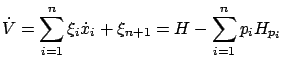 |
(7.16) |
where we applied the HJB equation (7.15) one more time to arrive at the second equality. (Actually, it is also easy to obtain this result directly by writing
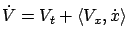 .) It is the equation (7.16) that enables a solution of the HJB equation via the method of characteristics. We know that the Cauchy problem for the HJB equation is given by
.) It is the equation (7.16) that enables a solution of the HJB equation via the method of characteristics. We know that the Cauchy problem for the HJB equation is given by
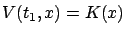 , where
, where 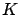 is the terminal cost and
is the terminal cost and 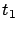 is the terminal time (this initial value problem involves flowing backward in time).
To calculate the value
is the terminal time (this initial value problem involves flowing backward in time).
To calculate the value 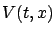 for some specific time
for some specific time 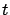 and state
and state  , we must first find a point
, we must first find a point
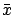 such that
such that 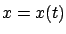 where
where
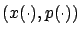 is the solution of the system of canonical equations with the boundary conditions
is the solution of the system of canonical equations with the boundary conditions
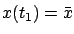 ,
,
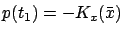 .
Then,
.
Then, 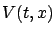 is computed by integration along the corresponding characteristic:
is computed by integration along the corresponding characteristic:
Again, the fact that 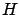 does not depend on
does not depend on 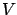 is helpful here. Figure 7.3 illustrates the procedure.
is helpful here. Figure 7.3 illustrates the procedure.
Figure:
Solving the HJB equation with the help of characteristics
|
|





Next: 7.3 Riccati equations and
Up: 7.2 HJB equation, canonical
Previous: 7.2.1 Method of characteristics
Contents
Index
Daniel
2010-12-20
![]() . Here it tells us that the value function satisfies
. Here it tells us that the value function satisfies