




Next: 7.2.2 Canonical equations as
Up: 7.2 HJB equation, canonical
Previous: 7.2 HJB equation, canonical
Contents
Index
Suppose that we are looking for a function
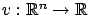 that
solves the PDE
that
solves the PDE
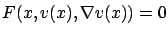 |
(7.9) |
where
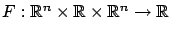 is a given continuous function.
This is the same equation as (5.34) but here we assume that
is a given continuous function.
This is the same equation as (5.34) but here we assume that 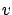 is differentiable in the classical sense. We are especially interested in the situation where
is differentiable in the classical sense. We are especially interested in the situation where 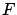 depends linearly on
depends linearly on 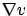 ; such PDEs are calledpartial differential equation (PDE)!quasi-linear quasi-linear. In addition, for simplicity and better geometric intuition, we start with the case when
; such PDEs are calledpartial differential equation (PDE)!quasi-linear quasi-linear. In addition, for simplicity and better geometric intuition, we start with the case when
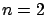 . Then (7.9) takes the form
. Then (7.9) takes the form
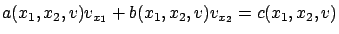 |
(7.10) |
for some functions 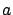 ,
, 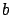 , and
, and 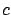 . Here and below, we omit some or all arguments of functions wherever convenient.
. Here and below, we omit some or all arguments of functions wherever convenient.
The graph of a solution
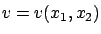 to (7.10) is a surface in the
to (7.10) is a surface in the
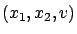 -space defined by the equation
-space defined by the equation
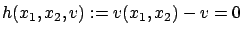 . The gradient vector
. The gradient vector
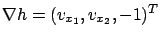 is normal to this surface at each point. Noting that the PDE (7.10) can be equivalently written as
is normal to this surface at each point. Noting that the PDE (7.10) can be equivalently written as
we conclude that the vector 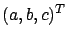 is everywhere orthogonal
to the normal
is everywhere orthogonal
to the normal 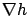 , hence it lies in the tangent space to the
solution surface. This is the geometric interpretation of the quasi-linear PDE (7.10): the vector field
, hence it lies in the tangent space to the
solution surface. This is the geometric interpretation of the quasi-linear PDE (7.10): the vector field 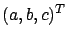 is tangent to the solution
surface
is tangent to the solution
surface
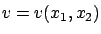 at each point. The system of ODEs associated with this vector field can be written as
at each point. The system of ODEs associated with this vector field can be written as
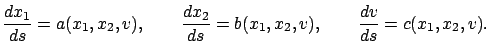 |
(7.11) |
These are called the characteristic ODEs of the PDE (7.10), and their solution curves are called the
characteristics. With a slight abuse of terminology, we sometimes use the term ``characteristics" not only for the solution curves of the equations (7.11) but also for these equations themselves.
The characteristic curves ``fill" our solution surface
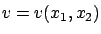 ; skipping ahead to Figure 7.2 may help the reader visualize this situation. As an example, it is useful to think about the case when
; skipping ahead to Figure 7.2 may help the reader visualize this situation. As an example, it is useful to think about the case when 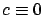 . Then (7.10) says that the derivative of
. Then (7.10) says that the derivative of 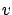 in the direction of the vector
in the direction of the vector 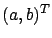 is 0, implying that
is 0, implying that 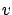 stays constant along solutions of the equations
stays constant along solutions of the equations
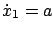 ,
,
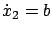 .
Every function
.
Every function  whose level sets are solution curves of these two equations in the
whose level sets are solution curves of these two equations in the 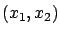 -plane is a solution of the PDE, and
the characteristics are horizontal slices of the corresponding solution surface.
Of course, in general (for nonzero
-plane is a solution of the PDE, and
the characteristics are horizontal slices of the corresponding solution surface.
Of course, in general (for nonzero 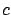 ) characteristics are
not horizontal.
) characteristics are
not horizontal.
Now, in principle we should be able to solve the characteristic ODEs and obtain the
characteristics. How does this help us
solve the original PDE (7.10)? Without additional specifications, there are ``too many" characteristics to identify a desired solution surface
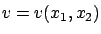 ; indeed, there is a characteristic passing through every point in the
; indeed, there is a characteristic passing through every point in the
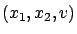 -space, so they fill the entire space. We know that
for ODEs, to fix a particular solution we must specify a point through
which it passes (an initial condition). The counterpart of this for the PDE (7.10) is that we must
specify a suitable curve in the
-space, so they fill the entire space. We know that
for ODEs, to fix a particular solution we must specify a point through
which it passes (an initial condition). The counterpart of this for the PDE (7.10) is that we must
specify a suitable curve in the
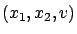 -space through which the
solution surface passes; we then obtain what is called a Cauchy (initial value) problem. Geometrically, the idea is that characteristics that pass
through points on this initial curve will determine the solution surface of the PDE, as illustrated in Figure 7.2 (with the thick curve representing an initial curve).
-space through which the
solution surface passes; we then obtain what is called a Cauchy (initial value) problem. Geometrically, the idea is that characteristics that pass
through points on this initial curve will determine the solution surface of the PDE, as illustrated in Figure 7.2 (with the thick curve representing an initial curve).
Figure:
Characteristics for an initial value problem
|
|
An initial curve can be defined in parametric form as
where
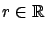 .
Then, the desired characteristics--i.e., the solutions of the characteristic equations (7.11) whose initial conditions lie on this initial curve--are
given by
.
Then, the desired characteristics--i.e., the solutions of the characteristic equations (7.11) whose initial conditions lie on this initial curve--are
given by
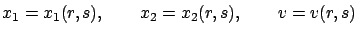 |
(7.12) |
which yields a description of the solution surface of our PDE (7.10).
However, we are looking for a different representation of this surface, namely,
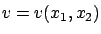 . To bring (7.12) to the desired form, we need to
express
. To bring (7.12) to the desired form, we need to
express 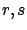 as functions of
as functions of 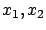 and plug them into
and plug them into 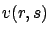 . For this to be possible, the map
. For this to be possible, the map
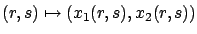 must be invertible. It follows from the Inverse Function Theorem that invertibility of this map, at least in some neighborhood of the initial curve, is in turn guaranteed if the corresponding Jacobian matrix
must be invertible. It follows from the Inverse Function Theorem that invertibility of this map, at least in some neighborhood of the initial curve, is in turn guaranteed if the corresponding Jacobian matrix
is nonsingular along the initial curve.
What is the geometric significance of this latter condition?
The columns of the above Jacobian matrix are the 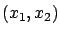 -components of the tangent vectors to the initial curve and to a characteristic, respectively, and they must be linearly independent. In other words, when projected onto the
-components of the tangent vectors to the initial curve and to a characteristic, respectively, and they must be linearly independent. In other words, when projected onto the 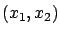 -plane, the characteristics and the initial curve must be transversal to each other. We conclude that under this
transversality condition, the Cauchy problem
for (7.10) is (locally) uniquely solvable, at least in principle, via the method of
characteristics.
To calculate the actual value of
-plane, the characteristics and the initial curve must be transversal to each other. We conclude that under this
transversality condition, the Cauchy problem
for (7.10) is (locally) uniquely solvable, at least in principle, via the method of
characteristics.
To calculate the actual value of
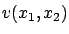 for some specific
for some specific 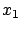 and
and 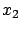 , we need to find a characteristic that connects the initial curve to a point with these
, we need to find a characteristic that connects the initial curve to a point with these 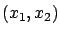 -coordinates and then integrate the last equation in (7.11) along that characteristic segment. We will discuss this procedure in more detail later
for the case of the HJB equation.
-coordinates and then integrate the last equation in (7.11) along that characteristic segment. We will discuss this procedure in more detail later
for the case of the HJB equation.
Characteristics can also be defined for the general PDE (7.9) which for 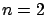 takes the form
takes the form
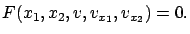 |
(7.13) |
In the case of the quasi-linear PDE (7.10), we saw that the tangent vector 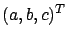 to the solution surface does not depend on
the partial derivatives
to the solution surface does not depend on
the partial derivatives 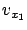 and
and 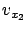 (which give the first two components of the normal vector
(which give the first two components of the normal vector
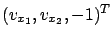 to this surface); consequently, the characteristic equations (7.11) involve
to this surface); consequently, the characteristic equations (7.11) involve 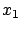 ,
, 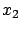 , and
, and 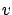 only. For the more general PDE (7.13), this is no longer guaranteed and
so five differential equations--describing the joint evolution of the variables
only. For the more general PDE (7.13), this is no longer guaranteed and
so five differential equations--describing the joint evolution of the variables
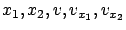 --are needed instead of three. The solution curves of these equations are called the characteristic strips. To simplify the notation, let us introduce the symbols
--are needed instead of three. The solution curves of these equations are called the characteristic strips. To simplify the notation, let us introduce the symbols
Then the characteristic strips are defined by the following equations:
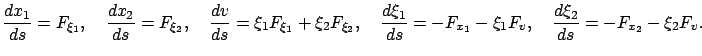 |
(7.14) |
We do not give a complete derivation of (7.14) but note that the first three equations in (7.14) reduce to the earlier characteristic equations (7.11) in the case of the quasi-linear PDE (7.10), whereas to arrive at the fourth equation in (7.14) it is enough to write
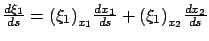 , use the first two characteristic equations to rewrite this result as
, use the first two characteristic equations to rewrite this result as
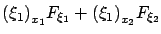 , and then apply the identity
, and then apply the identity
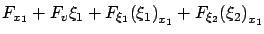 which follows by differentiating the PDE (7.13) with respect to
which follows by differentiating the PDE (7.13) with respect to 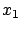 ; the last equation in (7.14) is derived in the same manner.
The last two equations in (7.14), which describe the evolution of the normal vector to the solution surface of the PDE, will play an important role in the next subsection where we turn to the HJB equation.
; the last equation in (7.14) is derived in the same manner.
The last two equations in (7.14), which describe the evolution of the normal vector to the solution surface of the PDE, will play an important role in the next subsection where we turn to the HJB equation.
In the above discussion we assumed that the independent variable  lives in the plane (i.e.,
lives in the plane (i.e., 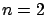 ). However, it is straightforward to write down the equations of the characteristic strips for a general dimension
). However, it is straightforward to write down the equations of the characteristic strips for a general dimension 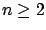 : we must simply replace the indices
: we must simply replace the indices 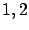 in (7.14) by
in (7.14) by
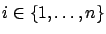 . In the next subsection we will work in this more general setting.
. In the next subsection we will work in this more general setting.





Next: 7.2.2 Canonical equations as
Up: 7.2 HJB equation, canonical
Previous: 7.2 HJB equation, canonical
Contents
Index
Daniel
2010-12-20
![]() that
solves the PDE
that
solves the PDE
![]() to (7.10) is a surface in the
to (7.10) is a surface in the
![]() -space defined by the equation
-space defined by the equation
![]() . The gradient vector
. The gradient vector
![]() is normal to this surface at each point. Noting that the PDE (7.10) can be equivalently written as
is normal to this surface at each point. Noting that the PDE (7.10) can be equivalently written as
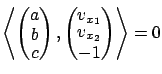
![]() ; skipping ahead to Figure 7.2 may help the reader visualize this situation. As an example, it is useful to think about the case when
; skipping ahead to Figure 7.2 may help the reader visualize this situation. As an example, it is useful to think about the case when ![]() . Then (7.10) says that the derivative of
. Then (7.10) says that the derivative of ![]() in the direction of the vector
in the direction of the vector ![]() is 0, implying that
is 0, implying that ![]() stays constant along solutions of the equations
stays constant along solutions of the equations
![]() ,
,
![]() .
Every function
.
Every function ![]() whose level sets are solution curves of these two equations in the
whose level sets are solution curves of these two equations in the ![]() -plane is a solution of the PDE, and
the characteristics are horizontal slices of the corresponding solution surface.
Of course, in general (for nonzero
-plane is a solution of the PDE, and
the characteristics are horizontal slices of the corresponding solution surface.
Of course, in general (for nonzero ![]() ) characteristics are
not horizontal.
) characteristics are
not horizontal.
![]() ; indeed, there is a characteristic passing through every point in the
; indeed, there is a characteristic passing through every point in the
![]() -space, so they fill the entire space. We know that
for ODEs, to fix a particular solution we must specify a point through
which it passes (an initial condition). The counterpart of this for the PDE (7.10) is that we must
specify a suitable curve in the
-space, so they fill the entire space. We know that
for ODEs, to fix a particular solution we must specify a point through
which it passes (an initial condition). The counterpart of this for the PDE (7.10) is that we must
specify a suitable curve in the
![]() -space through which the
solution surface passes; we then obtain what is called a Cauchy (initial value) problem. Geometrically, the idea is that characteristics that pass
through points on this initial curve will determine the solution surface of the PDE, as illustrated in Figure 7.2 (with the thick curve representing an initial curve).
-space through which the
solution surface passes; we then obtain what is called a Cauchy (initial value) problem. Geometrically, the idea is that characteristics that pass
through points on this initial curve will determine the solution surface of the PDE, as illustrated in Figure 7.2 (with the thick curve representing an initial curve).
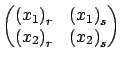
![]() takes the form
takes the form
![]() lives in the plane (i.e.,
lives in the plane (i.e., ![]() ). However, it is straightforward to write down the equations of the characteristic strips for a general dimension
). However, it is straightforward to write down the equations of the characteristic strips for a general dimension ![]() : we must simply replace the indices
: we must simply replace the indices ![]() in (7.14) by
in (7.14) by
![]() . In the next subsection we will work in this more general setting.
. In the next subsection we will work in this more general setting.