To illustrate the hybrid maximum principle, we apply it to the familiar light reflection example from Section 2.1.2. We model the propagation of a light ray through the ![]() -dimensional space via the control system
-dimensional space via the control system
We seek to derive a necessary condition for a trajectory ![]() that starts at a given initial point
that starts at a given initial point ![]() at time
at time ![]() , gets reflected off
, gets reflected off ![]() at some time
at some time ![]() , and arrives at a given final point
, and arrives at a given final point ![]() at time
at time ![]() to be locally time-optimal
with respect to trajectories that hit
to be locally time-optimal
with respect to trajectories that hit ![]() at nearby points.
This optimal control problem is not inherently hybrid, since (7.38) is a standard control system and it is capable of producing reflected trajectories. However, the classical formulation of the maximum principle does not allow us to incorporate the fact that we are only interested in trajectories that hit
at nearby points.
This optimal control problem is not inherently hybrid, since (7.38) is a standard control system and it is capable of producing reflected trajectories. However, the classical formulation of the maximum principle does not allow us to incorporate the fact that we are only interested in trajectories that hit ![]() along the way.
With the hybrid formulation, it is easy to do so by considering a hybrid system with a single discrete state location
along the way.
With the hybrid formulation, it is easy to do so by considering a hybrid system with a single discrete state location ![]() (i.e.,
(i.e., ![]() ) and the guard
) and the guard
![]() . In this hybrid system, discrete transitions occur when the trajectory hits
. In this hybrid system, discrete transitions occur when the trajectory hits ![]() , but the underlying control system (7.38) does not change and the trajectory remains continuous. The switching sequence associated with our candidate optimal trajectory
, but the underlying control system (7.38) does not change and the trajectory remains continuous. The switching sequence associated with our candidate optimal trajectory ![]() is
is ![]() , and the hybrid maximum principle captures local optimality over nearby trajectories with the same switching sequence--which is precisely what we want.
, and the hybrid maximum principle captures local optimality over nearby trajectories with the same switching sequence--which is precisely what we want.
Applying the hybrid maximum principle to this problem entails just a few straightforward computations. The Hamiltonian is
![]() . The Hamiltonian maximization condition gives
. The Hamiltonian maximization condition gives
![]() and
and
![]() . Since the final time is free, we have
. Since the final time is free, we have
![]() which in view of the nontriviality condition implies that
which in view of the nontriviality condition implies that
![]() and
and
![]() for all
for all ![]() . Normalizing them so that
. Normalizing them so that ![]() , we obtain
, we obtain
![]() hence
hence
![]() . Both the costate
. Both the costate ![]() and the optimal control
and the optimal control ![]() are continuous except possibly at the switching time
are continuous except possibly at the switching time ![]() . Since there is no switching cost, the switching condition tells us that
the vector
. Since there is no switching cost, the switching condition tells us that
the vector
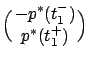 must be orthogonal to the
tangent space to
must be orthogonal to the
tangent space to ![]() at
at
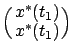 . This tangent space is
. This tangent space is ![]() itself, and vectors in it have the form
itself, and vectors in it have the form
![]() . It follows that
. It follows that
![]() for
for
![]() ; in other words,
; in other words,
![]() are continuous at
are continuous at ![]() , hence so are
, hence so are
![]() . Only the last component of
. Only the last component of ![]() can be discontinuous at
can be discontinuous at ![]() . But since
. But since
![]() is to remain equal to 1, it must be that
is to remain equal to 1, it must be that
![]() , i.e.,
, i.e., ![]() either stays continuous or flips its sign at
either stays continuous or flips its sign at ![]() . Of these two options, only the latter is possible because the light ray cannot pass through
. Of these two options, only the latter is possible because the light ray cannot pass through ![]() . We conclude that the velocity vectors before and after the reflection differ only in the component orthogonal to the reflection surface, and the difference is only in the minus sign. We have of course recovered the well-known law of reflection.
. We conclude that the velocity vectors before and after the reflection differ only in the component orthogonal to the reflection surface, and the difference is only in the minus sign. We have of course recovered the well-known law of reflection.