7.1.2 Re-interpreting the maximum principle

Suppose that we are given a (time-invariant) control system

$$\dot x=f(x,u)$$ (7.2)

whose state $x$ takes values in some $k$ -dimensional manifold $M$ and whose control $u$ takes values in some control set $U$ . For its solution $x(\cdot)$ to stay in $M$ , the velocity vector $f(x,u)$ must be tangent to $M$ at $x$ for all $x$ and $u$ . Thus we see that there is an important difference between the states and the velocity vectors: the former live in $M$ while the latter live in the tangent bundle $TM$ . When we worked over $\mathbb{R}^n$ , which is its own tangent space, we never explicitly made this distinction. In local coordinates, the system description takes the form

$$\begin{pmatrix} \dot x_1 \\ \vdots \\ \dot x_k \\ \end{pmat... ...{pmatrix} f_1(x,u) \\ \vdots \\ f_k(x,u) \\ \end{pmatrix}\in\mathbb{R}^k$$

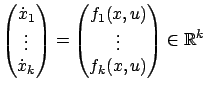
and the difference between states and tangent vectors becomes ``hidden" once again.

Let us assume for simplicity that an optimal control problem is formulated in the Mayer form (i.e., with terminal cost only). We know that problems with running cost can always be converted to this form by appending an additional state $x^0$ , which would yield a system on the augmented manifold $\mathbb{R}\times M$ (cf. Sections 3.3.2 and 4.2.1). The basic ingredients of the maximum principle are the costate $p$ and the Hamiltonian $H$ . In the case when $M=\mathbb{R}^n$ , the Hamiltonian for the Mayer problem took the form $H(x,u,p)=\langle p, f(x,u)\rangle$ . For a general manifold $M$ , we need to ask ourselves which space $p$ should belong to and how $H$ should be (re)defined. Our first natural guess might be that $p$ , like $f(x,u)$ , should be a tangent vector to $M$ . However, in contrast with $f(x,u)$ , there is no clear geometric reason why $p$ should be a tangent vector. Also, taking $p$ to be a tangent vector, we cannot assign a new meaning to our earlier definition of $H$ unless we equip the tangent space with an inner product. (Introducing an inner product on each tangent space $T_xM$ --called a Riemannian metric on $M$ --is possible but, as we will see, is neither necessary nor relevant for our present purposes.) Another option that might come to mind is that $p$ should live in $M$ itself; however, this choice offers even fewer clues towards any natural interpretation of the Hamiltonian.

Can we perhaps take a more direct guidance from the fact that in our old definition of the Hamiltonian, $p$ appears in an inner product with the velocity vector $f(x,u)$ ? In fact, we already remarked in Section 3.4.2 that $p$ never appears by itself but always inside inner products such as $\langle p,\dot x\rangle$ ; in other words, it acts on velocity vectors. This observation suggests that the intrinsic role of the costate $p$ is not that of a tangent vector, but that of a covector. To better understand the difference between these two types of objects and why the latter one correctly captures the notion of a costate, let us look at how they propagate along a flow induced by a dynamical system on $M$ .

Fix a number $\tau>0$ and let $\Phi_{\tau}: M\to M$ be a $\mathcal C^1$ map. While the construction that we are about to describe is valid for every such map, the map that we have in mind here is the one obtained by flowing forward for $\tau$ units of time along the trajectory of the system (7.2) corresponding to some fixed control $u$ (which, ultimately, is taken to be an optimal control for a given initial condition). Let us first discuss the transformation that $\Phi_{\tau}$ induces on tangent vectors. Pick a point $x\in M$ and a tangent vector $\xi\in T_x M$ . We know that $\xi$ is tangent to some curve in $M$ passing through $x$ , namely, $\xi=\dot x(0)$ where $x(\alpha)\in M$ for real $\alpha$ (around 0) and $x(0)=x$ . The image $\Phi_{\tau}(x(\cdot))$ of this curve under the map $\Phi_{\tau}$ is a curve in $M$ which passes through $\Phi_{\tau}(x)$ , as illustrated in Figure 7.1. Denote the tangent vector at $\Phi_{\tau}(x)$ associated with this new curve by $\left.d\Phi_{\tau}\right\vert _{x}(\xi)$ ; in other words, define

$$\left.d\Phi_{\tau}\right\vert _{x}(\xi):=\left.\frac d{d\alpha}\right\vert _{\alpha=0}\Phi_{\tau}(x(\alpha)).$$

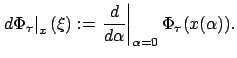
The above quantity depends only on the vector $\xi$ and not on the choice of a particular curve $x(\cdot)$ with this tangent vector. In this way we obtain a natural definition of a linear map

$$\left.d\Phi_{\tau}\right\vert _{x}: T_x M\to T_{\Phi_{\tau}(x)} M$$

called the derivative (or differential) of $\Phi_{\tau}$ at $x$ . It extends to manifolds the standard notion of the differential of a function (described by its Jacobian matrix) from vector calculus; more generally, functions from $M$ to another manifold $N$ can be considered, and we already discussed the case $N=\mathbb{R}$ in Section 7.1.1. In fact, in the proof of the maximum principle we performed a closely related computation, showing that an infinitesimal state perturbation $\xi$ propagates along an optimal trajectory of (7.2) according to the variational equation

$$\dot \xi =\left.{f}_{x}\right\vert _{*} \xi$$ (7.3)

(see Section 4.2.4). The derivative map ${d\Phi_{\tau}}$ pushes the tangent vectors forward in the direction of action of the original map $\Phi_{\tau}$ on $M$ . Objects such as tangent vectors, which propagate forward along a flow on $M$ in this sense, are called contravariant.

Figure: Tangent vectors propagate forward

Now suppose that we are given a covector at $x$ , i.e., a linear function on $T_xM$ . Let us denote it by $\left.p\right\vert _{x}$ so as to have $\left.p\right\vert _{x}(\xi)\in\mathbb{R}$ for each $\xi\in T_x M$ . For the same map $\Phi_{\tau}: M\to M$ as before, can we define in a natural way a linear function $\left.p\right\vert _{\Phi_{\tau}(x)}$ on $T_{\Phi_{\tau}(x)} M$ ? We must decide what the value $\left.p\right\vert _{\Phi_{\tau}(x)}(\eta)$ should be for every $\eta\in T_{\Phi_{\tau}(x)} M$ . While it is tempting to say that $\left.p\right\vert _{\Phi_{\tau}(x)}(\eta)$ should equal the value of $\left.p\right\vert _{x}$ on the preimage of $\eta$ under the map $\Phi_{\tau}$ , this preimage is not well defined unless the map $\Phi_{\tau}$ is invertible. In fact, the reader will quickly realize that there is no apparent candidate map for propagating covectors along $\Phi_{\tau}$ similarly to how the derivative map $d\Phi_{\tau}$ acts on tangent vectors. The reason is that, instead of trying to push covectors forward, we should pull them back. This revised objective is readily accomplished as follows: given a covector $\left.p\right\vert _{\Phi_{\tau}(x)}$ on $T_{\Phi_{\tau}(x)} M$ , define a covector $\left.p\right\vert _{x}$ on $T_xM$ by

$$\left.p\right\vert _{x}(\xi):= \left.p\right\vert _{\Phi_{\tau}(x)}(\left.d\Phi_{\tau}\right\vert _{x}(\xi)).$$ (7.4)

As we indicated earlier, the intended meaning of $\Phi_{\tau}$ is that of flowing forward for $\tau$ units of time along an optimal trajectory of (7.2), and the infinitesimal (as $\tau\to 0$ ) transformation induced by the derivative map $d\Phi_{\tau}$ is the variational equation (7.3). We can now recognize the formula (7.4) as expressing--in an intrinsic, coordinate-free fashion--the adjoint property from Section 4.2.8; indeed, it guarantees that $p(\xi)$ stays constant along the trajectory. The familiar adjoint equation $\dot p=-\big.{\left({f}_{x}\right)^T}\big\vert _*p$ is nothing but the infinitesimal version of (7.4) written in local coordinates. A fact not really revealed by this differential equation is that covectors are covariant objects, in the sense that they propagate backward along a flow on $M$ . This is exactly why we always have terminal rather than initial conditions for the costate!

Now everything is beginning to fall into place. The Hamiltonian for our Mayer problem on a manifold $M$ should be defined as

$$H(x,u,p)=p(f(x,u))$$ (7.5)

where the costate $p$ is a covector at $x$ (strictly speaking, it would be more accurate to write it as $\left.p\right\vert _{x}$ ). The maximum principle postulates the existence of a costate $p^*(t)\in T_{x^*(t)}^*M$ for each $t$ , where $x^*$ is the optimal trajectory being analyzed. The terminal value $p^*(t_f)$ uniquely specifies $p^*(t)$ for all $t\in[t_0,t_f]$ as explained above. The Hamiltonian maximization condition takes the same form as in Chapter 4. For a formal statement of the maximum principle on manifolds along these lines, see the references listed in Section 7.5. There is, however, one more concept that is usually involved when such results are stated in the literature, and we examine it briefly in the next subsection.