




Next: 1.4 Notes and references
Up: 1.3 Preview of infinite-dimensional
Previous: 1.3.3 Second variation and
Contents
Index
1.3.4 Global minima and convex problems
Regarding global minima of 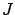 over a set
over a set
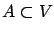 , much of
the discussion on global minima given at the end of
Section 1.2.1 carries over to the present case. In
particular, the Weierstrass Theorem is still valid,
provided that compactness of
, much of
the discussion on global minima given at the end of
Section 1.2.1 carries over to the present case. In
particular, the Weierstrass Theorem is still valid,
provided that compactness of 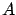 is understood in the sense of the
second or third definition given on page
is understood in the sense of the
second or third definition given on page ![[*]](crossref.gif) (existence of finite subcovers or sequential compactness). These
two definitions of compactness are equivalent for linear vector
spaces equipped with a norm (or, more generally, a metric). On the
other hand, closed and bounded subsets of an infinite-dimensional
vector space are not necessarily compact--we already mentioned
noncompactness of the unit sphere--and the Weierstrass Theorem
does not apply to them; see the next exercise. We note that since
our function space
(existence of finite subcovers or sequential compactness). These
two definitions of compactness are equivalent for linear vector
spaces equipped with a norm (or, more generally, a metric). On the
other hand, closed and bounded subsets of an infinite-dimensional
vector space are not necessarily compact--we already mentioned
noncompactness of the unit sphere--and the Weierstrass Theorem
does not apply to them; see the next exercise. We note that since
our function space 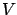 has a norm, the notions of continuity of
has a norm, the notions of continuity of
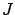 and convergence, closedness, boundedness, and openness in
and convergence, closedness, boundedness, and openness in 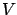 with respect to this norm are defined exactly as their familiar
counterparts in
with respect to this norm are defined exactly as their familiar
counterparts in
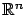 . We leave it to the reader to write down
precise definitions or consult the references given at the end of
this chapter.
. We leave it to the reader to write down
precise definitions or consult the references given at the end of
this chapter.

If 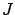 is a convex functional and
is a convex functional and
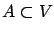 is a convex set, then the
optimization problem enjoys the same properties as the ones mentioned
at the end of Section 1.2.1 for finite-dimensional convex problems.
Namely, a local minimum is automatically a global one, and the
first-order necessary condition is also a sufficient condition for a minimum.
(Convexity of a functional and convexity of a subset of an
infinite-dimensional linear vector space are defined exactly
as the corresponding standard notions in the finite-dimensional case.) However, imposing extra
assumptions to ensure
convexity of
is a convex set, then the
optimization problem enjoys the same properties as the ones mentioned
at the end of Section 1.2.1 for finite-dimensional convex problems.
Namely, a local minimum is automatically a global one, and the
first-order necessary condition is also a sufficient condition for a minimum.
(Convexity of a functional and convexity of a subset of an
infinite-dimensional linear vector space are defined exactly
as the corresponding standard notions in the finite-dimensional case.) However, imposing extra
assumptions to ensure
convexity of 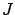 would severely
restrict the classes of problems that we
want to study. In this book, we focus on general theory that applies
to not necessarily convex problems; we will not directly use results from
convex optimization.
Nevertheless, some basic concepts
from (finite-dimensional) convex analysis will be important for us later,
particularly when we
derive the maximum principle.
would severely
restrict the classes of problems that we
want to study. In this book, we focus on general theory that applies
to not necessarily convex problems; we will not directly use results from
convex optimization.
Nevertheless, some basic concepts
from (finite-dimensional) convex analysis will be important for us later,
particularly when we
derive the maximum principle.





Next: 1.4 Notes and references
Up: 1.3 Preview of infinite-dimensional
Previous: 1.3.3 Second variation and
Contents
Index
Daniel
2010-12-20
![[*]](crossref.gif) (existence of finite subcovers or sequential compactness). These
two definitions of compactness are equivalent for linear vector
spaces equipped with a norm (or, more generally, a metric). On the
other hand, closed and bounded subsets of an infinite-dimensional
vector space are not necessarily compact--we already mentioned
noncompactness of the unit sphere--and the Weierstrass Theorem
does not apply to them; see the next exercise. We note that since
our function space
(existence of finite subcovers or sequential compactness). These
two definitions of compactness are equivalent for linear vector
spaces equipped with a norm (or, more generally, a metric). On the
other hand, closed and bounded subsets of an infinite-dimensional
vector space are not necessarily compact--we already mentioned
noncompactness of the unit sphere--and the Weierstrass Theorem
does not apply to them; see the next exercise. We note that since
our function space 