6.2.1 Existence and properties of the limit

We begin by making a series of observations about the behavior of $P(t_0,t_1)$ as a function of $t_1$ , with the goal of establishing that $\lim_{t_1\to\infty}P(t_0,t_1)$ exists (under the additional assumption of controllability) and has some interesting properties. This path will eventually lead us to a complete solution of the infinite-horizon LQR problem.

MONOTONICITY. It is not hard to see that the finite-horizon optimal cost $x_0^TP(t_0,t_1)x_0$ is a monotonically nondecreasing function of the final time $t_1$ . Indeed, let $t_2>t_1$ . Using (6.25), the definition of the value function, and the standing assumptions that $Q\ge 0$ and $R>0$ , we have

$$\begin{multline*} x_0^TP(t_0,t_2)x_0=V^{t_2}(t_0,x_0)=\int_{t_0}^{t_2} \left((x^... ...)Ru^*_{t_2}(t)\right)dt\ge V^{t_1}(t_0,x_0)=x_0^TP(t_0, t_1)x_0. \end{multline*}$$

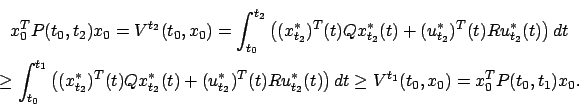
BOUNDEDNESS. It is not true in general that the optimal cost $x_0^TP(t_0,t_1)x_0$ remains bounded as $t_1\to\infty$ . For example, if the system is $\dot x=x$ (no control) then its solutions are growing exponentials and the infinite-horizon cost is clearly unbounded. However, we now show that the finite-horizon optimal cost $x_0^TP(t_0,t_1)x_0$ remains bounded as $t_1\to\infty$ assuming that $(A,B)$ is a controllable pair. Indeed, controllability guarantees the existence of a time $\bar t$ and a control $\bar u$ that steers the state from $x_0$ at time $t_0$ to 0 at time $\bar t$ . After time $\bar t$ , set $\bar u$ equal to 0. This control yields a state trajectory $\bar x$ satisfying $\bar x(t)=0$ for all $t\ge \bar t$ , and we have

$$x_0^TP(t_0,t_1)x_0=V^{t_1}(t_0,x_0)\le J(\bar u)=\int_{t_0}^{\bar... ... x^T(t)Q\bar x(t)+\bar u^T(t)R\bar u(t)\right)dt\qquad \forall\,t_1\ge \bar t.$$

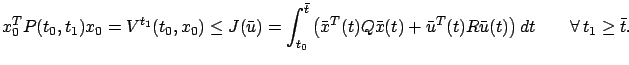
Since the above integral does not depend on $t_1$ , it provides a uniform bound for the optimal cost--a single bound that is valid for all sufficiently large $t_1$ , as desired. We leave the controllability assumption in force for the rest of this chapter (except for Exercise 6.5 on page  where its necessity will be re-examined).

EXISTENCE OF THE LIMIT. From the previous two claims it immediately follows that $x_0^TP(t_0,t_1)x_0$ has a limit as $t_1\to\infty$ . It turns out that more is true, namely, the matrix $\lim_{t_1\to\infty}P(t_0,t_1)$ is well defined. To see why, let us consider some specific initial conditions $x_0$ (we can do this because all the facts established so far are valid for arbitrary $x_0$ ). First, let $x_0=e_i$ with $e_i$ as defined on page  for some $i\in\{1,\dots,n\}$ . Then $x_0^TP(t_0,t_1)x_0=P_{ii}(t_0,t_1)$ , implying that each diagonal entry of $P(t_0,t_1)$ has a limit as ${t_1\to\infty}$ . Next, let $x_0=e_i+e_j$ for some $i\ne j$ . Recalling that $P(t_0,t_1)$ is symmetric (Exercise 6.2), we have $x_0^TP(t_0,t_1)x_0=P_{ii}(t_0,t_1)+2P_{ij}(t_0,t_1)+P_{jj}(t_0,t_1)$ , from which we can deduce that the off-diagonal entries of $P(t_0,t_1)$ converge as well. We can think of $\lim_{t_1\to\infty}P(t_0,t_1)$ as the solution of the RDE (6.14) that, starting from the zero matrix, has flown backward for infinite time and reached steady state; Figure 6.1 should help visualize this situation.

Figure: Steady-state solution of the RDE

PROPERTIES OF THE LIMIT. Since the RDE (6.14) is now a time-invariant differential equation, its solution $P(t_0,t_1)$ actually depends only on the difference $t_1-t_0$ . Thus it is clear that the steady-state solution $\lim_{t_1\to\infty}P(t_0,t_1)$ , whose existence we just established, does not depend on $t_0$ , i.e., it is a constant matrix. Denoting it simply by $P$ , we have

$$P=\lim_{t_1\to\infty} P(t,t_1) \qquad \forall\,t.$$ (6.26)

Next, passing to the limit as $t_1\to\infty$ on both sides of the RDE (6.14), we see that $\lim_{t_1\to\infty} \dot P(t,t_1)$ must also exist and be a constant matrix, which must then necessarily be the zero matrix. We thus conclude that $P$ is a solution of the algebraic Riccati equation (ARE)

$$\fbox{$P A+A^TP +Q-P BR^{-1}B^TP =0$}$$ (6.27)

Conceptually, the step of passing from the RDE (6.14), which is a matrix differential equation, to the ARE (6.28), which is a static matrix equation, mirrors our earlier step of passing from the general HJB equation (5.10) to its infinite-horizon counterpart (5.19). In both cases, the time derivative is eliminated; in the present case, we are left with no derivatives at all! The ARE (6.28) can be solved analytically or numerically without difficulties. It may happen that the ARE has ``spurious" extra solutions other than (6.27). In this regard, it is useful to note that the matrix $P$ given by (6.27) must be symmetric positive semidefinite (because so is $P(t,t_1)$ for each $t_1$ ). We can hope that the ARE has only one solution with this additional property. This is the case in the next exercise, and we will show in Section 6.2.4 that this is always the case under appropriate assumptions.