




Next: 6.2.4 Complete result and
Up: 6.2 Infinite-horizon LQR problem
Previous: 6.2.2 Infinite-horizon problem and
Contents
Index
6.2.3 Closed-loop stability
In the previous subsection we were able to obtain a complete solution to the infinite-horizon LQR problem, under the assumption (enforced since Section 6.2.1) that the system is controllable.
Here we investigate an important property of the optimal closed-loop system which will motivate us to introduce one more
assumption.

An optimal control that causes the state to grow unbounded is hardly acceptable.
The reason for this undesirable situation in the above example is that the cost only takes into account the control effort and does not penalize
instability. It is natural to ask under what additional assumption(s) the optimal control (6.31) automatically ensures that the state converges to 0.
One option is to require 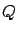 to be strictly positive definite, but we will see in a moment that this would be an overkill. It is well known and easy to show (for example, via diagonalization) that every symmetric positive semidefinite matrix
to be strictly positive definite, but we will see in a moment that this would be an overkill. It is well known and easy to show (for example, via diagonalization) that every symmetric positive semidefinite matrix 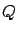 can be written as
can be written as
where 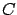 is a
is a
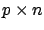 matrix with
matrix with 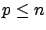 .
Introducing the auxiliary output
.
Introducing the auxiliary output
we can rewrite the cost (6.29) as
Let us now assume that our system is observable through this output, i.e., assume that 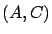 is an observable pair.
Note that if
is an observable pair.
Note that if 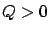 then
then 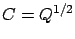 (matrix square root) which is
(matrix square root) which is 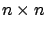 and
nonsingular, and the observability assumption automatically holds. On the
other hand, in Example 6.2 we had
and
nonsingular, and the observability assumption automatically holds. On the
other hand, in Example 6.2 we had 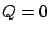 hence
hence 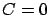 and the observability
assumption fails.
and the observability
assumption fails.
It is not difficult to see why observability guarantees that the optimal closed-loop system is asymptotically stable. We know from (6.32) that the optimal control 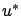 gives a bounded cost (for arbitrary
gives a bounded cost (for arbitrary 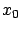 ). This cost is
). This cost is
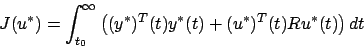 |
(6.32) |
where
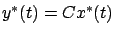 is the output along the optimal trajectory. Next, recall that
is the output along the optimal trajectory. Next, recall that 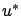 is generated by the linear feedback law (6.31), which means that the optimal closed-loop system is a linear time-invariant system. Its solution
is generated by the linear feedback law (6.31), which means that the optimal closed-loop system is a linear time-invariant system. Its solution 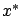 is thus given by a linear combination of (complex) exponential functions of time, and the same is true about
is thus given by a linear combination of (complex) exponential functions of time, and the same is true about 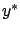 and
and 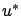 . This observation and the fact that
. This observation and the fact that 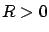 make it clear that in order for the integral in (6.33) to be bounded we must have
make it clear that in order for the integral in (6.33) to be bounded we must have
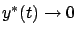 and
and
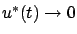 as
as
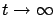 . It is well known that if the output and the input of an observable linear time-invariant system converge to 0, then so does the state. (One way to see this is as follows: by observability, there exists a matrix
. It is well known that if the output and the input of an observable linear time-invariant system converge to 0, then so does the state. (One way to see this is as follows: by observability, there exists a matrix  such that
such that 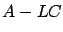 has arbitrary desired eigenvalues with negative real parts; rewriting the system dynamics as
has arbitrary desired eigenvalues with negative real parts; rewriting the system dynamics as
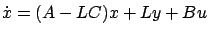 , it is easy to show that
, it is easy to show that 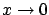 when
when 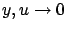 .) Therefore, the optimal closed-loop system must be asymptotically--in fact, exponentially--stable.
.) Therefore, the optimal closed-loop system must be asymptotically--in fact, exponentially--stable.





Next: 6.2.4 Complete result and
Up: 6.2 Infinite-horizon LQR problem
Previous: 6.2.2 Infinite-horizon problem and
Contents
Index
Daniel
2010-12-20

![]() to be strictly positive definite, but we will see in a moment that this would be an overkill. It is well known and easy to show (for example, via diagonalization) that every symmetric positive semidefinite matrix
to be strictly positive definite, but we will see in a moment that this would be an overkill. It is well known and easy to show (for example, via diagonalization) that every symmetric positive semidefinite matrix ![]() can be written as
can be written as 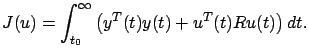
![]() gives a bounded cost (for arbitrary
gives a bounded cost (for arbitrary ![]() ). This cost is
). This cost is