




Next: 6.2.1 Existence and properties
Up: 6. The Linear Quadratic
Previous: 6.1.4 Global existence of
Contents
Index
6.2 Infinite-horizon LQR problem
The infinite-horizon version of the LQR problem is a special case of the general infinite-horizon problem constructed in Section 5.1.3. Starting with the finite-horizon LQR problem defined in Section 6.1, we first
assume that both the control system and the cost functional are time-invariant and that there is no terminal cost; this simply means that 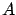 ,
, 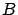 ,
, 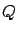 , and
, and 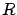 are now constant matrices and
are now constant matrices and 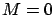 . Then, we want to consider the limit as the final time
. Then, we want to consider the limit as the final time 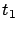 approaches
approaches 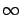 . The resulting problem does not directly fit into the basic problem formulation of Section 3.3 and its well-posedness needs to be proved; in particular, we do not know a priori whether the optimal cost is finite (cf. footnote 2 on page
. The resulting problem does not directly fit into the basic problem formulation of Section 3.3 and its well-posedness needs to be proved; in particular, we do not know a priori whether the optimal cost is finite (cf. footnote 2 on page ![[*]](crossref.gif) ). We did not try to settle this issue in the general context of Section 5.1.3, but we will do it here for the LQR problem. In this section we assume that the reader is familiar with basic concepts of linear system theory such as controllability and observability.
). We did not try to settle this issue in the general context of Section 5.1.3, but we will do it here for the LQR problem. In this section we assume that the reader is familiar with basic concepts of linear system theory such as controllability and observability.
In preparation for studying the limit as
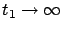 , let us treat the final time
, let us treat the final time 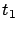 as a parameter which, unlike in Section 6.1, is no longer fixed. We want to make our notation more explicit by displaying the dependence of relevant quantities on this parameter. Specifically, from now on let us write
as a parameter which, unlike in Section 6.1, is no longer fixed. We want to make our notation more explicit by displaying the dependence of relevant quantities on this parameter. Specifically, from now on let us write  for the value function and denote by
for the value function and denote by 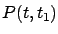 the solution at time
the solution at time 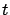 of the RDE (6.14) with the boundary condition
of the RDE (6.14) with the boundary condition  . For each
. For each 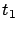 , let us also relabel the optimal control and the optimal state trajectory (passing through the given initial condition
, let us also relabel the optimal control and the optimal state trajectory (passing through the given initial condition 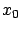 at time
at time 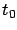 ) for the corresponding finite-horizon LQR problem as
) for the corresponding finite-horizon LQR problem as 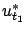 and
and  , respectively. In this notation, the results of Section 6.1.3 say that
, respectively. In this notation, the results of Section 6.1.3 say that
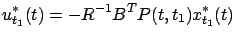 |
(6.23) |
and
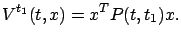 |
(6.24) |
In particular,
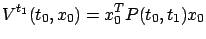 |
(6.25) |
is the finite-horizon optimal cost.
Subsections





Next: 6.2.1 Existence and properties
Up: 6. The Linear Quadratic
Previous: 6.1.4 Global existence of
Contents
Index
Daniel
2010-12-20
![[*]](crossref.gif) ). We did not try to settle this issue in the general context of Section 5.1.3, but we will do it here for the LQR problem. In this section we assume that the reader is familiar with basic concepts of linear system theory such as controllability and observability.
). We did not try to settle this issue in the general context of Section 5.1.3, but we will do it here for the LQR problem. In this section we assume that the reader is familiar with basic concepts of linear system theory such as controllability and observability.