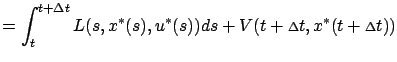Next: 5.1.3.1 Infinite-horizon problem
Up: 5.1 Dynamic programming and
Previous: 5.1.2 Principle of optimality
Contents
Index
5.1.3 HJB equation
In the principle of optimality (5.4) the value
function 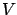 appears on both sides with different arguments. We
can thus think of (5.4) as describing a dynamic
relationship among the optimal values of the
costs (5.1) for different
appears on both sides with different arguments. We
can thus think of (5.4) as describing a dynamic
relationship among the optimal values of the
costs (5.1) for different 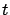 and
and  , which we declared earlier
to be our goal. However, this relationship is rather clumsy and not very
convenient to use in its present form. What we will now do is pass
to its more compact infinitesimal
version, which will take the form of a partial differential equation (PDE).
The steps that follow rely on first-order Taylor
expansions; the reader will recall that
we used somewhat similar calculations when deriving the
maximum principle.
First, write
, which we declared earlier
to be our goal. However, this relationship is rather clumsy and not very
convenient to use in its present form. What we will now do is pass
to its more compact infinitesimal
version, which will take the form of a partial differential equation (PDE).
The steps that follow rely on first-order Taylor
expansions; the reader will recall that
we used somewhat similar calculations when deriving the
maximum principle.
First, write
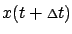 appearing on the right-hand side
of (5.4) as
appearing on the right-hand side
of (5.4) as
where we remembered that 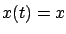 . This allows us to express
. This allows us to express
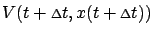 as
as
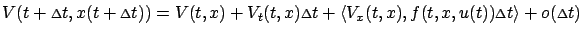 |
(5.7) |
(for now we proceed under the assumption--whose validity we will examine later--that 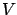 is
is
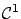 .)
We also have
.)
We also have
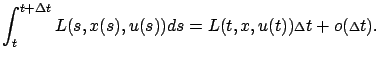 |
(5.8) |
Substituting the expressions given by (5.7)
and (5.8) into the right-hand side of (5.4),
we obtain
The two 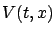 terms cancel out (because the one inside the infimum
does not depend on
terms cancel out (because the one inside the infimum
does not depend on  and can be pulled outside), which leaves us with
and can be pulled outside), which leaves us with
![$\displaystyle 0=\inf_{u_{[t,t+\Delta t]}}\left\{L(t,x,u(t)){\scriptstyle\Delta}...
...t,x),f(t,x,u(t)){\scriptstyle\Delta}t\rangle +o({\scriptstyle\Delta}t)\right\}.$](img1594.gif) |
(5.9) |
Let us now divide
by
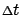 and take it to be small. In the limit as
and take it to be small. In the limit as
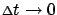 the higher-order term
the higher-order term
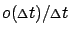 disappears,
and the infimum is taken
over the instantaneous value of
disappears,
and the infimum is taken
over the instantaneous value of  at time
at time 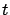 (in fact, already in (5.9) the control values
(in fact, already in (5.9) the control values 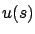 for
for 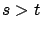 affect the expression inside the infimum only through the
affect the expression inside the infimum only through the
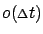 term).
Pulling
term).
Pulling
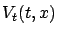 outside the infimum as it does not depend on
outside the infimum as it does not depend on  , we conclude that the equation
, we conclude that the equation
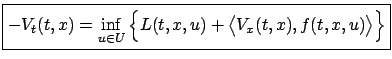 |
(5.10) |
must hold for all
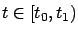 and all
and all
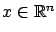 .
This equation for the value function is called the Hamilton-Jacobi-Bellman
(HJB) equation. It is a PDE since it contains partial derivatives of
.
This equation for the value function is called the Hamilton-Jacobi-Bellman
(HJB) equation. It is a PDE since it contains partial derivatives of 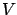 with respect to
with respect to
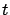 and
and  . The accompanying boundary condition is (5.3).
. The accompanying boundary condition is (5.3).
Note that the terminal cost appears only in the boundary
condition and not in the HJB equation itself. In fact, the specifics about
the terminal cost and terminal time did not play a role in our derivation
of the HJB equation. For different target sets,
the boundary condition changes (as
we already discussed) but the HJB equation remains the same. However, the HJB equation will not hold for
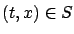 just like it does not hold at
just like it does not hold at 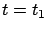 in the fixed-time case, because the principle of optimality is not valid there.
in the fixed-time case, because the principle of optimality is not valid there.
We can apply one more transformation in order to rewrite the
HJB equation in a simpler--and also more insightful--way. It is
easy to check that (5.10) is equivalent to
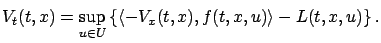 |
(5.11) |
Let us now recall our earlier
definition (3.29) of the Hamiltonian,
reproduced here:
We see that the expression inside the supremum in (5.11) is
nothing but the Hamiltonian, with 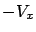 playing the role of
the costate. This brings us to the Hamiltonian form of the HJB equation:
playing the role of
the costate. This brings us to the Hamiltonian form of the HJB equation:
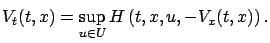 |
(5.12) |
So far, the existence of an optimal control has not been assumed.
When an optimal (in the global sense) control 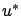 does exist, the infimum in the
previous calculations can be replaced by a minimum and this
minimum is achieved when
does exist, the infimum in the
previous calculations can be replaced by a minimum and this
minimum is achieved when 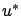 is plugged in. In particular, the
principle of optimality (5.4) yields
is plugged in. In particular, the
principle of optimality (5.4) yields
where
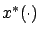 and
and 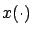 are trajectories corresponding
to
are trajectories corresponding
to
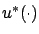 and
and 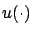 , respectively, both passing through
the same point
, respectively, both passing through
the same point 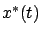 at time
at time 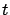 . From this, repeating the
same steps that led us earlier to the HJB equation (5.10),
we obtain
. From this, repeating the
same steps that led us earlier to the HJB equation (5.10),
we obtain
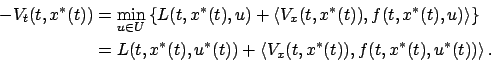 |
(5.13) |
Expressed in terms of the Hamiltonian, the second equation in (5.13) becomes
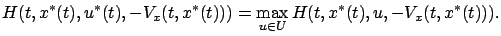 |
(5.14) |
This Hamiltonian maximization condition is analogous to the one we
had in the maximum principle. We see that if we can find a closed-form expression for the control that maximizes the Hamiltonian--or, equivalently, the control that achieves the infimum in the HJB equation (5.10)--then the HJB equation becomes simpler and more explicit.
 5.1
5.1

Subsections





Next: 5.1.3.1 Infinite-horizon problem
Up: 5.1 Dynamic programming and
Previous: 5.1.2 Principle of optimality
Contents
Index
Daniel
2010-12-20
![]() appears on both sides with different arguments. We
can thus think of (5.4) as describing a dynamic
relationship among the optimal values of the
costs (5.1) for different
appears on both sides with different arguments. We
can thus think of (5.4) as describing a dynamic
relationship among the optimal values of the
costs (5.1) for different ![]() and
and ![]() , which we declared earlier
to be our goal. However, this relationship is rather clumsy and not very
convenient to use in its present form. What we will now do is pass
to its more compact infinitesimal
version, which will take the form of a partial differential equation (PDE).
The steps that follow rely on first-order Taylor
expansions; the reader will recall that
we used somewhat similar calculations when deriving the
maximum principle.
First, write
, which we declared earlier
to be our goal. However, this relationship is rather clumsy and not very
convenient to use in its present form. What we will now do is pass
to its more compact infinitesimal
version, which will take the form of a partial differential equation (PDE).
The steps that follow rely on first-order Taylor
expansions; the reader will recall that
we used somewhat similar calculations when deriving the
maximum principle.
First, write
![]() appearing on the right-hand side
of (5.4) as
appearing on the right-hand side
of (5.4) as
![]() just like it does not hold at
just like it does not hold at ![]() in the fixed-time case, because the principle of optimality is not valid there.
in the fixed-time case, because the principle of optimality is not valid there.
![]() does exist, the infimum in the
previous calculations can be replaced by a minimum and this
minimum is achieved when
does exist, the infimum in the
previous calculations can be replaced by a minimum and this
minimum is achieved when ![]() is plugged in. In particular, the
principle of optimality (5.4) yields
is plugged in. In particular, the
principle of optimality (5.4) yields
![$\displaystyle =\min_{u_{[t,t+\Delta t]}}\left\{\int_t^{t+{\scriptstyle\Delta}t} L( s,x(s),u(s))d s+V(t+{\scriptstyle\Delta}t,x(t+{\scriptstyle\Delta}t))\right\}$](img1609.gif)