




Next: 6.1.4 Global existence of
Up: 6.1 Finite-horizon LQR problem
Previous: 6.1.2 Riccati differential equation
Contents
Index
6.1.3 Value function and optimality
We now proceed to show that the control law (6.12) identified by the maximum principle is globally optimal. We already asked the reader to examine this issue via a direct analysis of the second variation in part b) of Exercise 3.8. Since then, however, we learned a general method for establishing optimality--namely, the sufficient condition for
optimality from Section 5.1.4--and it is instructive to see it in action here.
Specialized to our present LQR problem, the
HJB equation (5.10) becomes
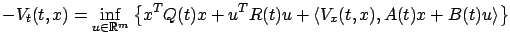 |
(6.15) |
and the boundary condition (5.3) reads
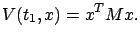 |
(6.16) |
Since 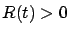 , it is easy to see that the infimum of the quadratic function of
, it is easy to see that the infimum of the quadratic function of  in (6.16) is a minimum and to calculate (similarly to how we arrived at the formula (6.3) earlier) that the minimizing control is
in (6.16) is a minimum and to calculate (similarly to how we arrived at the formula (6.3) earlier) that the minimizing control is
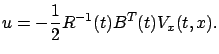 |
(6.17) |
We substitute this control into (6.16) and, after some term cancellations, bring the HJB equation to the following form:
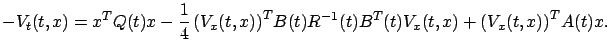 |
(6.18) |
In order to apply the sufficient condition for optimality proved in Section 5.1.4, we need to find a solution
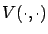 of (6.19). Then, for the feedback law (6.12) to be optimal, it should match the feedback law given by (6.18) for this
of (6.19). Then, for the feedback law (6.12) to be optimal, it should match the feedback law given by (6.18) for this 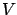 . (The precise meaning of the last statement is provided by the formula (5.22) on page
. (The precise meaning of the last statement is provided by the formula (5.22) on page ![[*]](crossref.gif) .) This will in turn be true if we have
.) This will in turn be true if we have
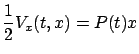 |
(6.19) |
for all 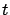 and
and  . The equation (6.20) suggests that we should look for a function
. The equation (6.20) suggests that we should look for a function 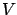 that is defined in terms of
that is defined in terms of  . Another observation that supports this idea is that in view of (6.11), the boundary condition (6.17) for the HJB equation can be written as
. Another observation that supports this idea is that in view of (6.11), the boundary condition (6.17) for the HJB equation can be written as
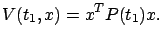 |
(6.20) |
Armed with these facts, let us apply a certain amount of ``wishful thinking" in solving the partial differential equation (6.19). Namely, let us try to guess a function 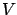 that satisfies the simple conditions (6.20) and (6.21), and then see if it satisfies the complicated equation (6.19). If it does, then it must be the value function and by the previous reasoning our control (6.12) must be optimal, hence everything will be proved. (In this last step, we are using the fact that (6.12) is a feedback law which does not depend on the initial condition; see the remarks immediately following the proof of the sufficient condition for optimality on page
that satisfies the simple conditions (6.20) and (6.21), and then see if it satisfies the complicated equation (6.19). If it does, then it must be the value function and by the previous reasoning our control (6.12) must be optimal, hence everything will be proved. (In this last step, we are using the fact that (6.12) is a feedback law which does not depend on the initial condition; see the remarks immediately following the proof of the sufficient condition for optimality on page ![[*]](crossref.gif) .)
.)
For the moment, let us proceed under the assumption (which will be validated momentarily) that 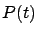 is symmetric for all
is symmetric for all 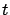 . A guess for
. A guess for 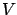 is actually fairly obvious, and might have already occurred to the reader:
is actually fairly obvious, and might have already occurred to the reader:
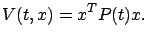 |
(6.21) |
This function clearly satisfies (6.21), and since its gradient with respect to  is
is
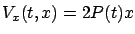 we see that (6.20) is also fulfilled. Now, let us check whether the function (6.22) satisfies (6.19). Since
we see that (6.20) is also fulfilled. Now, let us check whether the function (6.22) satisfies (6.19). Since
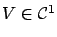 , the viscosity solution concept is not needed here.
Noting that
, the viscosity solution concept is not needed here.
Noting that
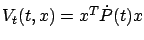 and plugging the two expressions for the partial derivatives of
and plugging the two expressions for the partial derivatives of 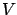 into (6.19), we obtain
into (6.19), we obtain
or, equivalently,
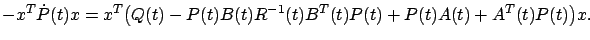 |
(6.22) |
Since 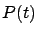 satisfies the RDE (6.14), it immediately follows that (6.23) is a true identity. We conclude that, indeed, the function (6.22) is the value function (optimal cost-to-go) and the linear feedback law (6.12) is the optimal control. (We already know from Section 6.1.1 that an optimal control must be unique, and we also know that the sufficient condition of Section 5.1.4 guarantees global optimality.)
satisfies the RDE (6.14), it immediately follows that (6.23) is a true identity. We conclude that, indeed, the function (6.22) is the value function (optimal cost-to-go) and the linear feedback law (6.12) is the optimal control. (We already know from Section 6.1.1 that an optimal control must be unique, and we also know that the sufficient condition of Section 5.1.4 guarantees global optimality.)
It is useful to reflect on how we found the optimal control.
First, we singled out a candidate optimal control by using the maximum principle. Second, we identified a candidate value function and verified that this function and the candidate control satisfy the sufficient condition for optimality. Thus we followed the typical path outlined in Section 5.1.4.
The next exercise takes a closer look at properties of 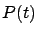 and closes a gap that we left in the above argument.
and closes a gap that we left in the above argument.

It was both insightful and convenient to employ the sufficient condition for optimality in terms of the HJB equation to find the expression for the optimal cost and confirm optimality of the control (6.12). However, having the solution 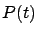 of the RDE (6.14)
with the boundary condition (6.11) in hand, it is also possible to solve the LQR problem by direct algebraic manipulations without relying on any prior theory.
of the RDE (6.14)
with the boundary condition (6.11) in hand, it is also possible to solve the LQR problem by direct algebraic manipulations without relying on any prior theory.






Next: 6.1.4 Global existence of
Up: 6.1 Finite-horizon LQR problem
Previous: 6.1.2 Riccati differential equation
Contents
Index
Daniel
2010-12-20
![]() of (6.19). Then, for the feedback law (6.12) to be optimal, it should match the feedback law given by (6.18) for this
of (6.19). Then, for the feedback law (6.12) to be optimal, it should match the feedback law given by (6.18) for this ![]() . (The precise meaning of the last statement is provided by the formula (5.22) on page
. (The precise meaning of the last statement is provided by the formula (5.22) on page ![[*]](crossref.gif) .) This will in turn be true if we have
.) This will in turn be true if we have
![[*]](crossref.gif) .)
.)
![]() is symmetric for all
is symmetric for all ![]() . A guess for
. A guess for ![]() is actually fairly obvious, and might have already occurred to the reader:
is actually fairly obvious, and might have already occurred to the reader:
![]() and closes a gap that we left in the above argument.
and closes a gap that we left in the above argument.
![]() of the RDE (6.14)
with the boundary condition (6.11) in hand, it is also possible to solve the LQR problem by direct algebraic manipulations without relying on any prior theory.
of the RDE (6.14)
with the boundary condition (6.11) in hand, it is also possible to solve the LQR problem by direct algebraic manipulations without relying on any prior theory.
