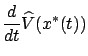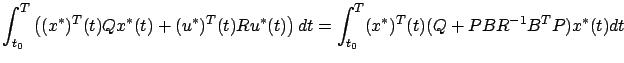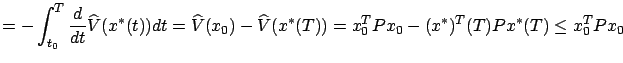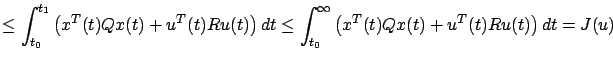Next: 6.2.3 Closed-loop stability
Up: 6.2 Infinite-horizon LQR problem
Previous: 6.2.1 Existence and properties
Contents
Index
6.2.2 Infinite-horizon problem and its solution
We have now prepared the ground for taking the limit as
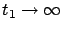 and considering the infinite-horizon LQR problem with the cost
and considering the infinite-horizon LQR problem with the cost
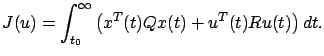 |
(6.28) |
Recalling the optimal cost (6.26)
and the optimal control (6.24)
for the finite-horizon case, and passing to the limit as
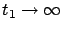 ,
it is natural to guess that the infinite-horizon optimal cost and optimal control will be6.3
,
it is natural to guess that the infinite-horizon optimal cost and optimal control will be6.3
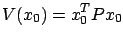 |
(6.29) |
and
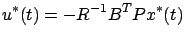 |
(6.30) |
where  is the matrix limit (6.27) which satisfies the ARE (6.28). Note that the quadratic cost (6.30) is independent of
is the matrix limit (6.27) which satisfies the ARE (6.28). Note that the quadratic cost (6.30) is independent of 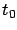 and the linear feedback law (6.31) is time-invariant, which is consistent with the problem formulation and with our earlier findings in Section 5.1.3. Still, optimality of (6.31) is far from obvious, and it is not even clear whether a control yielding a bounded cost exists. Strictly speaking, the use of the asterisks in (6.31) is not yet justified; at this point,
and the linear feedback law (6.31) is time-invariant, which is consistent with the problem formulation and with our earlier findings in Section 5.1.3. Still, optimality of (6.31) is far from obvious, and it is not even clear whether a control yielding a bounded cost exists. Strictly speaking, the use of the asterisks in (6.31) is not yet justified; at this point, 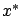 is simply the trajectory of the system under the action of the feedback law (6.31) with
is simply the trajectory of the system under the action of the feedback law (6.31) with
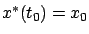 .
.
We now show that the above guess is indeed correct. Consider the function
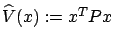 . Its derivative along
the trajectory
. Its derivative along
the trajectory 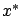 is
is
where the last equality follows from the ARE (6.28).
We can then calculate the portion of the corresponding cost over an arbitrary finite interval ![$ [t_0,T]$](img1918.gif) to be
to be
where the last inequality follows from the fact that 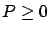 . Taking the limit
as
. Taking the limit
as
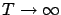 , we obtain
, we obtain
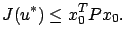 |
(6.31) |
In particular, we can now be sure that the infinite-horizon problem is well posed, because 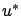 gives a bounded cost.
On the other hand, consider another trajectory
gives a bounded cost.
On the other hand, consider another trajectory  with the same initial condition corresponding to an arbitrary control
with the same initial condition corresponding to an arbitrary control  . Since
. Since
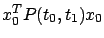 is the finite-horizon optimal cost, we have for every finite
is the finite-horizon optimal cost, we have for every finite 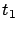 that
that
where the second inequality relies on the positive (semi)definiteness of 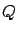 and
and
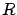 . Passing to the limit as
. Passing to the limit as
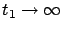 yields
yields
Comparing this inequality with (6.32) and remembering that  was arbitrary (and could in particular be equal to
was arbitrary (and could in particular be equal to 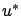 ), we see that
), we see that
hence
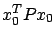 is the infinite-horizon optimal cost and
is the infinite-horizon optimal cost and 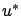 is an optimal control, as claimed.
is an optimal control, as claimed.





Next: 6.2.3 Closed-loop stability
Up: 6.2 Infinite-horizon LQR problem
Previous: 6.2.1 Existence and properties
Contents
Index
Daniel
2010-12-20
![]() and considering the infinite-horizon LQR problem with the cost
and considering the infinite-horizon LQR problem with the cost
![]() . Its derivative along
the trajectory
. Its derivative along
the trajectory ![]() is
is