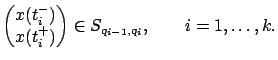Next: 7.4.2 Hybrid maximum principle
Up: 7.4 Maximum principle for
Previous: 7.4 Maximum principle for
Contents
Index
7.4.1 Hybrid optimal control problem
We begin by defining the class of hybrid control systems and associated optimal control problems that we want to study.
The first ingredient of our hybrid control system is a collection of (time-invariant) control systems
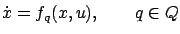 |
(7.32) |
where 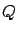 is a finite index set; for simplicity, we assume that all the systems in the collection (7.32) share the same state space
is a finite index set; for simplicity, we assume that all the systems in the collection (7.32) share the same state space
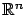 and control set
and control set
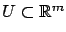 . The second ingredient is a collection of switching surfaces (or guards)
. The second ingredient is a collection of switching surfaces (or guards)
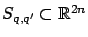 , one for each pair
, one for each pair
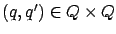 . A function
. A function
![$ x:[t_0,t_f]\to\mathbb{R}^n$](img2173.gif) is an admissible trajectory of our hybrid system corresponding to a control
is an admissible trajectory of our hybrid system corresponding to a control
![$ u:[t_0,t_f]\to U$](img2174.gif) if there exist time instants
if there exist time instants
and indices
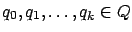 such that
such that 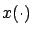 satisfies
satisfies
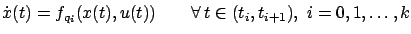 |
(7.33) |
and
Here 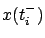 and
and 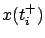 are the values of
are the values of  right before and right after
right before and right after 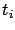 , respectively, and the value
, respectively, and the value 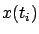 is taken to be equal to one of these one-sided limits, depending on the desired convention. At each possible discontinuity
is taken to be equal to one of these one-sided limits, depending on the desired convention. At each possible discontinuity 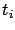 , a discrete transition (or switching event) is said to occur.
The function
, a discrete transition (or switching event) is said to occur.
The function
![$ q:[t_0,t_f]\to Q$](img2183.gif) defined by
defined by 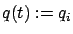 for
for
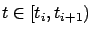 describes the evolution of
describes the evolution of 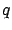 along the trajectory;
along the trajectory; 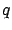 is often called the discrete state of the hybrid system. We can use it to rewrite (7.33) more concisely as
is often called the discrete state of the hybrid system. We can use it to rewrite (7.33) more concisely as
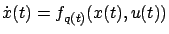 for
for 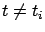 ,
,
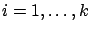 .
.
We consider cost functionals of the form
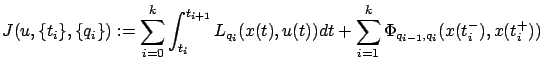 |
(7.34) |
where
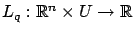 is the usual running cost and
is the usual running cost and
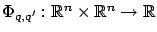 is the switching cost, for
is the switching cost, for 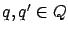 .
For simplicity, we do not include a terminal cost (this is no loss of generality, as terminal cost can be easily incorporated into the above running-plus-switching cost along the lines of Section 3.3.2).
We also introduce
an endpoint constraint, characterized by a set
.
For simplicity, we do not include a terminal cost (this is no loss of generality, as terminal cost can be easily incorporated into the above running-plus-switching cost along the lines of Section 3.3.2).
We also introduce
an endpoint constraint, characterized by a set
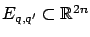 for each pair
for each pair
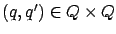 , according to which the trajectory
, according to which the trajectory 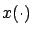 must satisfy
must satisfy
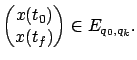 |
(7.35) |
(Here
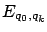 plays the same role as
plays the same role as 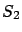 at the end of Section 4.3.1.)
Then, the hybrid optimal control problem consists in finding a control that minimizes the cost (7.34) subject to the endpoint constraint (7.35). We emphasize that the choice of a control
at the end of Section 4.3.1.)
Then, the hybrid optimal control problem consists in finding a control that minimizes the cost (7.34) subject to the endpoint constraint (7.35). We emphasize that the choice of a control  is accompanied by the choice of two finite sequences
is accompanied by the choice of two finite sequences 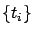 and
and 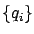 , to which we henceforth refer as the time sequence and switching sequence, respectively.
, to which we henceforth refer as the time sequence and switching sequence, respectively.





Next: 7.4.2 Hybrid maximum principle
Up: 7.4 Maximum principle for
Previous: 7.4 Maximum principle for
Contents
Index
Daniel
2010-12-20