7.1.3 Symplectic geometry and Hamiltonian flows

In our discussion of Hamiltonian mechanics in Section 2.4, the Hamiltonian was given a clear physical interpretation as the total energy of the system. Hamilton's canonical differential equations, on the other hand, were derived formally from the Euler-Lagrange equation and we never paused to consider their intrinsic meaning. We fill this gap here by exposing the important connection between symplectic geometry and Hamiltonian flows, which provides one further insight into the geometric formulation of the maximum principle.

Let us return to the cotangent bundle $T^* M$ which, as explained at the end of Section 7.1.1, is a $2k$ -dimensional manifold equipped with canonical local coordinates. On this manifold there is a natural differential 2-form $\omega^2$ , called a symplectic form (or symplectic structure). This is a bilinear skew-symmetric form on the tangent space to $T^* M$ at each point; in other words, it acts on pairs of tangent vectors to $T^* M$ (and, moreover, it depends smoothly on the choice of a point in $T^* M$ ). In canonical coordinates $(x,p)=(x_1,\dots,x_k,p_1,\dots,p_k)$ on $T^* M$ , the symplectic form that we consider here is given by

$$\omega^2:=dx_1\wedge dp_1+\dots+dx_k\wedge dp_k$$

where the exterior multiplication $\wedge$ is defined by

$$(\omega_1\wedge\omega_2)(\xi_1,\xi_2):= \omega_1(\xi_1)\omega_2(\xi_2)- \omega_2(\xi_1) \omega_1(\xi_2).$$

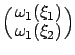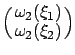(The exterior product is the oriented area spanned by the vectors $\Big({\textstyle{\omega_1(\xi_1)}\atop \textstyle{\omega_1(\xi_2)}}\Big)$ and $\Big({\textstyle{\omega_2(\xi_1)}\atop \textstyle{\omega_2(\xi_2)}}\Big)$ , or the determinant of the corresponding matrix.) Given two tangent vectors to $T^* M$ with components $(y,q)=(y_1,\dots,y_k,q_1,\dots,q_k)$ and $(z,r)=(z_1,\dots,z_k,r_1,\dots,r_k)$ , it is straightforward to check that

$$\omega^2\big((y,q),(z,r)\big)=\sum_{i=1}^k(y_ir_i-q_iz_i).$$ (7.6)

The symplectic form allows us to establish a one-to-one correspondence between tangent vectors to $T^* M$ and covectors on $T^* M$ , as follows. To a tangent vector $\xi$ (at a fixed point of $T^* M$ ) we associate a covector $\omega^1_\xi$ which acts on another tangent vector $\eta$ to $T^* M$ according to

$$\omega^1_\xi(\eta):=\omega^2(\xi,\eta).$$ (7.7)

The map $\xi\mapsto\omega^1_\xi$ is a linear map between vector spaces, whose matrix with respect to the canonical basis is $\begin{pmatrix} 0 & -I \\ I & 0\\ \end{pmatrix}$ .

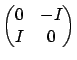Now, we can view our Hamiltonian (7.5) as a function on the cotangent bundle $T^* M$ (i.e., a function of the variables $x$ and $p$ ) parameterized additionally by the controls $u$ . Then the differential $dH$ of the Hamiltonian gives us a covector on $T^* M$ at each point. Applying the inverse of the map constructed above to this covector, we obtain a tangent vector at each point of $T^* M$ , or a vector field on $T^* M$ . This vector field is called the Hamiltonian vector field and is denoted by $\vec H$ . In canonical coordinates, the flow along $\vec H$ is described by the familiar differential equations

$$\dot x={H}_{p},\qquad \dot p=-{H}_{x}.$$ (7.8)

Indeed, for an arbitrary tangent vector $\eta$ to $T^* M$ with components $(z,r)=(z_1,\dots,z_k,r_1,\dots,r_k)$ , we can easily check using (7.6) that with $\vec H$ defined via (7.8) we have

$$\omega^2(\vec H,\eta)=\sum_{i=1}^k ({H}_{x_i}z_i+ {H}_{p_i}r_i)=dH(\eta)$$

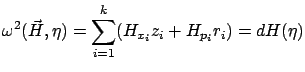
and the desired conclusion follows from (7.7). Therefore, the statement of the maximum principle about the existence of a costate satisfying the adjoint equation (the second canonical equation) can be reformulated as saying that an optimal state trajectory can be lifted to an integral curve of the Hamiltonian vector field. (The control $u$ remains an argument on the right-hand side of (7.8), but the maximum principle is of course applied with an optimal control $u^*$ plugged in.)