1.2.1.2 Second-order conditions for optimality

We now derive another necessary condition and also a sufficient condition for optimality, under the stronger hypothesis that $f$ is a $\mathcal C^2$ function (twice continuously differentiable).

First, we assume as before that $x^*$ is a local minimum and derive a necessary condition. For an arbitrary fixed $d\in\mathbb{R}^n$ , let us consider a Taylor expansion of $g(\alpha)=f(x^*+\alpha d)$ again, but this time include second-order terms:

$$g(\alpha)=g(0)+g'(0)\alpha+\frac12g''(0)\alpha^2+o(\alpha^2)$$ (1.12)

where

$$\lim_{\alpha\to 0}\frac{o(\alpha^2)}{\alpha^2}=0.$$ (1.13)

By the first-order necessary condition, $g'(0)$ must be 0 since it is given by (1.10). We claim that

$$g''(0)\ge 0.$$ (1.14)

Indeed, suppose that $g''(0)<0$ . By (1.13), there exists an $\varepsilon >0$ such that

$$\vert\alpha\vert<\varepsilon \quad\Rightarrow\quad \vert o(\alpha^2)\vert< \frac12\vert g''(0)\vert\alpha^2.$$

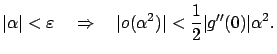
For these values of $\alpha$ , (1.12) reduces to $g(\alpha)-g(0)<0$ , contradicting that fact that 0 is a minimum of $g$ . Therefore, (1.14) must hold.

What does this result imply about the original function $f$ ? To see what $g''(0)$ is in terms of $f$ , we need to differentiate the formula (1.9). The reader may find it helpful to first rewrite (1.9) more explicitly as

$$g'(\alpha)=\sum_{i=1}^n {f}_{x_i}(x^*+\alpha d) d_i.$$

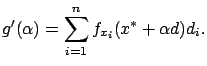
Differentiating both sides with respect to $\alpha$ , we have

$$g''(\alpha)=\sum_{i,j=1}^n {f}_{{x_i}{x_j}}(x^*+\alpha d) d_i d_j$$

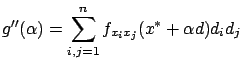
where double subscripts are used to denote second-order partial derivatives. For $\alpha=0$ this gives

$$g''(0)=\sum_{i,j=1}^n {f}_{{x_i}{x_j}}(x^*) d_i d_j$$

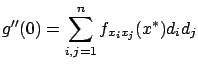
or, in matrix notation,

$$g''(0)=d^T\nabla^2 f(x^*)d$$ (1.15)

where

$$\nabla^2 f:= \begin{pmatrix} {f}_{{x_1}{x_1}} & \dots& {f}_{{x... ...n}} \\ &\ddots& \\ {f}_{{x_n}{x_1}} & \dots &{f}_{{x_n}{x_n}} \end{pmatrix}$$

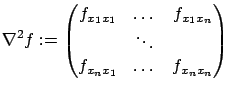
is the Hessian matrix of $f$ . In view of (1.14), (1.15), and the fact that $d$ was arbitrary, we conclude that the matrix $\nabla^2 f(x^*)$ must be positive semidefinite:

$$\fbox{$\nabla^2 f(x^*)\ge 0$} \$$    (positive semidefinite)

This is the second-order necessary condition for optimality.

Like the previous first-order necessary condition, this second-order condition only applies to the unconstrained case. But, unlike the first-order condition, it requires $f$ to be $\mathcal C^2$ and not just $\mathcal C^1$ . Another difference with the first-order condition is that the second-order condition distinguishes minima from maxima: at a local maximum, the Hessian must be negative semidefinite, while the first-order condition applies to any extremum (a minimum or a maximum).

Strengthening the second-order necessary condition and combining it with the first-order necessary condition, we can obtain the following second-order sufficient condition for optimality: If a $\mathcal C^2$ function $f$ satisfies

$$\nabla f(x^*)=0 \qquad \nabla^2 f(x^*)>0 \$$ (1.16)

on an interior point $x^*$ of its domain, then $x^*$ is a strict local minimum of $f$ . To see why this is true, take an arbitrary $d\in\mathbb{R}^n$ and consider again the second-order expansion (1.12) for $g(\alpha)=f(x^*+\alpha d)$ . We know that $g'(0)$ is given by (1.10), thus it is 0 because $\nabla f(x^*)=0$ . Next, $g''(0)$ is given by (1.15), and so we have

$$f(x^*+\alpha d)=f(x^*)+\frac12 d^T\nabla^2 f(x^*)d\alpha^2 +o(\alpha^2).$$ (1.17)

The intuition is that since the Hessian $\nabla^2 f(x^*)$ is a positive definite matrix, the second-order term dominates the higher-order term $o(\alpha^2)$ . To establish this fact rigorously, note that by the definition of $o(\alpha^2)$ we can pick an $\varepsilon >0$ small enough so that

$$\vert\alpha\vert<\varepsilon ,\ \alpha\ne 0 \quad\Rightarrow\quad \vert o(\alpha^2)\vert<\frac12 d^T\nabla^2 f(x^*)d\alpha^2$$

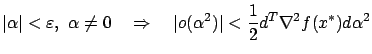
and for these values of $\alpha$ we deduce from (1.17) that $f(x^*+\alpha d)>f(x^*).$

To conclude that $x^*$ is a (strict) local minimum, one more technical detail is needed. According to the definition of a local minimum (see page ), we must show that $f(x^*)$ is the lowest value of $f$ in some ball around $x^*$ . But the term $o(\alpha^2)$ and hence the value of $\varepsilon$ in the above construction depend on the choice of the direction $d$ . It is clear that this dependence is continuous, since all the other terms in (1.17) are continuous in $d$ .^1.2Also, without loss of generality we can restrict $d$ to be of unit length, and then we can take the minimum of $\varepsilon$ over all such $d$ . Since the unit sphere in $\mathbb{R}^n$ is compact, the minimum is well defined (thanks to the Weierstrass Theorem which is discussed below). This minimal value of $\varepsilon$ provides the radius of the desired ball around $x^*$ in which the lowest value of $f$ is achieved at $x^*$ .