




Next: 1.2.1.1 First-order necessary condition
Up: 1.2 Some background on
Previous: 1.2 Some background on
Contents
Index
1.2.1 Unconstrained optimization
The term ``unconstrained optimization" usually refers to the situation where
all points  sufficiently near
sufficiently near 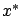 in
in
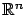 are in
are in 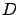 , i.e.,
, i.e., 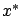 belongs to
belongs to 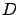 together with some
together with some
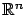 -neighborhood. The
simplest case is when
-neighborhood. The
simplest case is when
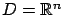 , which is sometimes called
the completely unconstrained case. However, as far as local
minimization is concerned, it is enough to assume that
, which is sometimes called
the completely unconstrained case. However, as far as local
minimization is concerned, it is enough to assume that 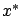 is an interior point
of
is an interior point
of 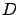 . This is automatically true if
. This is automatically true if 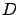 is an
open subset of
is an
open subset of
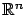 .
.
Subsections
Daniel
2010-12-20