




Next: 5.3.3 HJB equation and
Up: 5.3 Viscosity solutions of
Previous: 5.3.1 One-sided differentials
Contents
Index
5.3.2 Viscosity solutions of PDEs
We are now ready to introduce the concept of a viscosity solution for PDEs.
Consider a PDE of the form
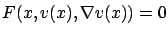 |
(5.30) |
where
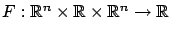 is a continuous function.
A viscosity subsolution of the
PDE (5.34)
is
a continuous function
is a continuous function.
A viscosity subsolution of the
PDE (5.34)
is
a continuous function
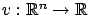 such that
such that
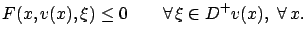 |
(5.31) |
As we know, this is equivalent to saying that at every  we must have
we must have
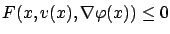 for every
for every
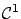 test
function
test
function 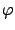 such that
such that  has a local minimum at
has a local minimum at
 . Similarly,
. Similarly, 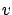 is a
viscosity supersolution of (5.34) if
is a
viscosity supersolution of (5.34) if
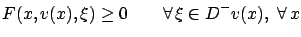 |
(5.32) |
or, equivalently, at every  we have
we have
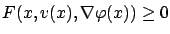 for every
for every
 function
function  such that
such that  has a local maximum at
has a local maximum at
 . Finally,
. Finally, 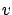 is a viscosity
solution if it is both a viscosity subsolution and a viscosity supersolution.
is a viscosity
solution if it is both a viscosity subsolution and a viscosity supersolution.
The above definitions of a viscosity subsolution and supersolution impose conditions on 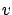 only
at points where
only
at points where 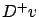 , respectively
, respectively 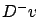 , is nonempty. We know that the
set of these points is dense in the domain of
, is nonempty. We know that the
set of these points is dense in the domain of 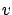 .
At all points where
.
At all points where 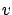 is differentiable, the PDE must hold in the classical
sense. If
is differentiable, the PDE must hold in the classical
sense. If 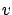 is Lipschitz, then by Rademacher's theorem it is differentiable almost everywhere.
is Lipschitz, then by Rademacher's theorem it is differentiable almost everywhere.
![\begin{Example}
Consider the scalar case ($n=1$) and let $F(x,v,\xi)=1-\vert\xi\...
...or all $\xi\in[-1,1]$, making~\eqref{e-supersol} true as well.~\qed\end{Example}](img1735.gif)
Note the lack of symmetry in the definition of a viscosity solution: the sign convention used when writing the PDE is important.
In the above example, if we rewrite the PDE as
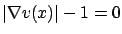 , then it is easy to see that
, then it is easy to see that 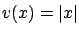 is no longer a viscosity solution.
is no longer a viscosity solution.
The terminology ``viscosity solutions" is motivated by the fact that a viscosity solution 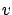 of the PDE (5.34) can be obtained
from smooth solutions
of the PDE (5.34) can be obtained
from smooth solutions
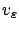 to the family of PDEs
to the family of PDEs
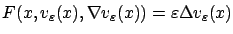 |
(5.33) |
(parameterized by
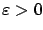 )
in the limit as
)
in the limit as
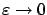 . The operator
. The operator 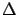 on the right-hand side of (5.37) denotes the Laplacian (
on the right-hand side of (5.37) denotes the Laplacian (
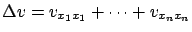 ); in fluid mechanics it appears in the PDE describing the motion of a viscous fluid. To understand the basic idea behind this convergence result, let
); in fluid mechanics it appears in the PDE describing the motion of a viscous fluid. To understand the basic idea behind this convergence result, let
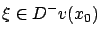 for some
for some 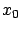 . Consider a test function
. Consider a test function 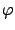 such that
such that
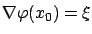 and
and  has a local maximum at
has a local maximum at
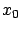 . Assume that
. Assume that
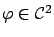 (if not, approximate it by a
(if not, approximate it by a
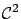 function).
If
function).
If
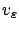 is close to
is close to 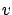 for small
for small
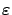 ,
then
,
then
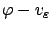 has a local maximum at some
has a local maximum at some
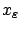 near
near 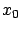 , implying that
, implying that
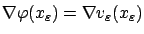 and
and
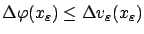 . Since
. Since
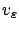 solves (5.37), this gives
solves (5.37), this gives
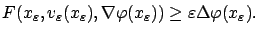 Taking the limit as
Taking the limit as
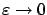 , by continuity of
, by continuity of 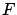 we have
we have
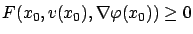 , which means that
, which means that 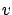 is a supersolution of (5.34). The argument showing that
is a supersolution of (5.34). The argument showing that 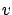 is a subsolution is similar.
is a subsolution is similar.





Next: 5.3.3 HJB equation and
Up: 5.3 Viscosity solutions of
Previous: 5.3.1 One-sided differentials
Contents
Index
Daniel
2010-12-20
![]() only
at points where
only
at points where ![]() , respectively
, respectively ![]() , is nonempty. We know that the
set of these points is dense in the domain of
, is nonempty. We know that the
set of these points is dense in the domain of ![]() .
At all points where
.
At all points where ![]() is differentiable, the PDE must hold in the classical
sense. If
is differentiable, the PDE must hold in the classical
sense. If ![]() is Lipschitz, then by Rademacher's theorem it is differentiable almost everywhere.
is Lipschitz, then by Rademacher's theorem it is differentiable almost everywhere.
![\begin{Example}
Consider the scalar case ($n=1$) and let $F(x,v,\xi)=1-\vert\xi\...
...or all $\xi\in[-1,1]$, making~\eqref{e-supersol} true as well.~\qed\end{Example}](img1735.gif)
![]() , then it is easy to see that
, then it is easy to see that ![]() is no longer a viscosity solution.
is no longer a viscosity solution.
![]() of the PDE (5.34) can be obtained
from smooth solutions
of the PDE (5.34) can be obtained
from smooth solutions
![]() to the family of PDEs
to the family of PDEs