Let
![]() be a continuous function (nothing beyond continuity is required from
be a continuous function (nothing beyond continuity is required from ![]() ).
A vector
).
A vector
![]() is called a super-differential of
is called a super-differential of
![]() at a given point
at a given point ![]() if for all
if for all ![]() near
near ![]() we have the relation
we have the relation
Similarly, we say that
![]() is a sub-differential of
is a sub-differential of ![]() at
at ![]() if
if
We now establish some useful properties of super- and sub-differentials.
TEST FUNCTIONS.
![]() if and only if there exists a
if and only if there exists a
![]() function
function
![]() such that
such that
![]() ,
,
![]() , and
, and
![]() for all
for all ![]() near
near
![]() , i.e.,
, i.e., ![]() has a
local minimum at
has a
local minimum at ![]() . Similarly,
. Similarly,
![]() if and only if there exists a
if and only if there exists a
![]() function
function ![]() such that
such that
![]() and
and ![]() has a
local maximum at
has a
local maximum at ![]() . (Note that we can always arrange to have
. (Note that we can always arrange to have
![]() by adding a constant to
by adding a constant to ![]() , which does not affect the other conditions.)
, which does not affect the other conditions.)
The function ![]() is sometimes called a test function. For the case of
is sometimes called a test function. For the case of ![]() , an example of such a function is shown in Figure 5.7. The above result, whose proof we will not give, will be used for proving the other facts that follow.
, an example of such a function is shown in Figure 5.7. The above result, whose proof we will not give, will be used for proving the other facts that follow.
RELATION WITH CLASSICAL DIFFERENTIALS. If ![]() is differentiable at
is differentiable at ![]() , then
, then
We prove both claims with the help of test functions. First, suppose that ![]() is differentiable at
is differentiable at ![]() . It is clear that the gradient
. It is clear that the gradient
![]() is both a super-differential and a sub-differential of
is both a super-differential and a sub-differential of ![]() at
at ![]() (indeed, with
(indeed, with
![]() both (5.31) and (5.32) become equalities).
If
both (5.31) and (5.32) become equalities).
If ![]() has a local minimum or maximum at
has a local minimum or maximum at ![]() for some
for some
![]() , then
, then
![]() hence
hence
![]() . This shows that
. This shows that
![]() is the only element in
is the only element in ![]() and
and ![]() .
.
To prove the second claim,
let
![]() be such that
be such that
![]() and
and
![]() for
for ![]() near
near ![]() . Then
. Then
![]() has a local maximum at
has a local maximum at
![]() , implying that
, implying that
![]() hence
hence
![]() .
For
.
For ![]() (the case
(the case ![]() is completely analogous) we can write
is completely analogous) we can write
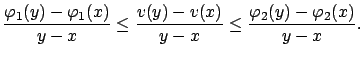
As
NON-EMPTINESS AND DENSENESS. The sets
![]() and
and
![]() are both nonempty, and actually dense in the domain of
are both nonempty, and actually dense in the domain of ![]() .
.
The idea of the proof is sketched in Figure 5.8. The highly irregular graph in the figure is that of ![]() . Take an arbitrary point
. Take an arbitrary point ![]() . Choosing a
. Choosing a
![]() function
function ![]() steep enough (see the solid curve in the figure), we can force
steep enough (see the solid curve in the figure), we can force
![]() to have a local maximum at a nearby point
to have a local maximum at a nearby point ![]() , as close to
, as close to
![]() as we want. (For clarity, we also shift the graph of
as we want. (For clarity, we also shift the graph of ![]() vertically to produce the dotted curve in the figure which touches the graph of
vertically to produce the dotted curve in the figure which touches the graph of ![]() at
at ![]() .) We then have
.) We then have
![]() . A similar argument works for
. A similar argument works for ![]() .
.
![]()