




Next: 7.4 Maximum principle for
Up: 7.3 Riccati equations and
Previous: 7.3.2 control problem
Contents
Index
As we have seen, a representative example of Riccati matrix inequalities encountered in robust control is
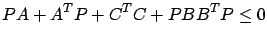 |
(7.30) |
(this is (7.26) with 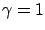 ). Similar Riccati inequalities arise in the context of several other control problems.
The inequality (7.30) is quadratic in the matrix variable
). Similar Riccati inequalities arise in the context of several other control problems.
The inequality (7.30) is quadratic in the matrix variable
 . However, it can be shown to be equivalent
to the linear matrix inequality (LMI)
. However, it can be shown to be equivalent
to the linear matrix inequality (LMI)
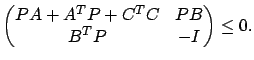 |
(7.31) |
The matrix on the left-hand side of (7.31) is called the Schur complement of the matrix on the left-hand side of (7.30).
The constraint 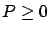 can also be naturally incorporated into this LMI.
can also be naturally incorporated into this LMI.
Being convex feasibility problems, LMIs can be efficiently solved by known numerical algorithms from convex optimization. Several dedicated software packages exist for solving LMIs. This makes conditions expressed in terms of LMIs attractive from the computational point of view.





Next: 7.4 Maximum principle for
Up: 7.3 Riccati equations and
Previous: 7.3.2 control problem
Contents
Index
Daniel
2010-12-20