




Next: 3.4.3 Second variation
Up: 3.4 Variational approach to
Previous: 3.4.1 Preliminaries
Contents
Index
3.4.2 First variation
We want to compute and analyze the first variation
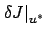 of the cost functional
of the cost functional 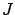 at the optimal control function
at the optimal control function 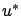 . To do this, in view of the definition (1.33), we must isolate the first-order terms with respect to
. To do this, in view of the definition (1.33), we must isolate the first-order terms with respect to 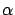 in the cost difference between the perturbed control (3.24) and the optimal control
in the cost difference between the perturbed control (3.24) and the optimal control 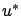 :
:
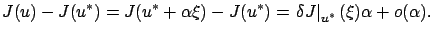 |
(3.30) |
The formula (3.30) suggests regarding the difference
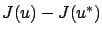 as being composed of three distinct terms, which we now inspect in more detail.
We will let
as being composed of three distinct terms, which we now inspect in more detail.
We will let  denote equality up to
terms of order
denote equality up to
terms of order 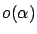 . For the terminal cost, we have
. For the terminal cost, we have
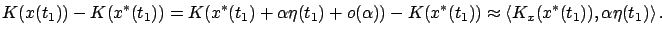 |
(3.31) |
For the Hamiltonian, omitting the 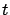 -arguments inside
-arguments inside  and
and  for brevity, we have
for brevity, we have
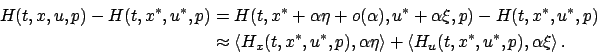 |
(3.32) |
As for the inner product
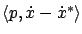 , we use integration by parts as we did several times in calculus of variations:
, we use integration by parts as we did several times in calculus of variations:
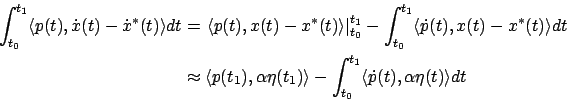 |
(3.33) |
where we used the fact that
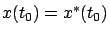 . Combining the formulas (3.30)-(3.34), we
readily see that the first variation is given by
. Combining the formulas (3.30)-(3.34), we
readily see that the first variation is given by
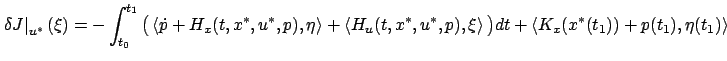 |
(3.34) |
where 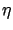 is related to
is related to 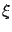 via the differential equation (3.27)
with the zero initial condition.
via the differential equation (3.27)
with the zero initial condition.
The familiar first-order necessary condition for optimality
(from Section 1.3.2) says that we must have
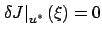 for all
for all 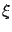 .
This condition is true for every function
.
This condition is true for every function 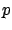 , but becomes
particularly revealing if we make a special choice of
, but becomes
particularly revealing if we make a special choice of 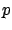 .
Namely, let
.
Namely, let 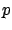 be
the solution of the differential equation
be
the solution of the differential equation
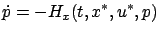 |
(3.35) |
satisfying the boundary condition
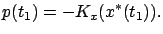 |
(3.36) |
Note that this boundary condition specifies the value of 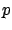 at
the end of the interval
at
the end of the interval ![$ [t_0,t_1]$](img803.gif) , i.e., it is a final (or terminal)
condition rather than an initial condition. In case of no terminal
cost we treat
, i.e., it is a final (or terminal)
condition rather than an initial condition. In case of no terminal
cost we treat  as being equal to 0, which corresponds to
as being equal to 0, which corresponds to
 . We label the function
. We label the function 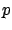 defined
by (3.36) and (3.37) as
defined
by (3.36) and (3.37) as 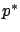 from now on, to
reflect the fact that it is associated with the optimal
trajectory. We also extend the notation
from now on, to
reflect the fact that it is associated with the optimal
trajectory. We also extend the notation
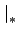 to mean evaluation
along the optimal trajectory with
to mean evaluation
along the optimal trajectory with 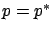 , so that, for example,
, so that, for example,
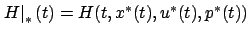 . Setting
. Setting 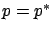 and
using the equations (3.36) and (3.37) to simplify
the right-hand side of (3.35), we are left with
and
using the equations (3.36) and (3.37) to simplify
the right-hand side of (3.35), we are left with
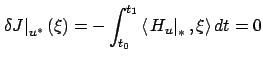 |
(3.37) |
for all 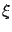 .
We know from Lemma 2.13.3 that this implies
.
We know from Lemma 2.13.3 that this implies
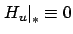 or, in more detail,
or, in more detail,
![$\displaystyle {H}_{u}(t,x^*(t),u^*(t),p^*(t))= 0\qquad \forall\,t\in[t_0,t_1].$](img923.gif) |
(3.38) |
The meaning of this condition is that the Hamiltonian has a stationary point
as a function
of  along the optimal trajectory. More precisely,
the function
along the optimal trajectory. More precisely,
the function
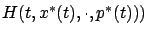 has a stationary point at
has a stationary point at 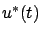 for all
for all 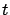 . This is just a reformulation of the
property already discussed in Section 2.4.1 in the context
of calculus of variations.
. This is just a reformulation of the
property already discussed in Section 2.4.1 in the context
of calculus of variations.
In light of the definition (3.29) of the Hamiltonian,
we can rewrite
our control system (3.18) more compactly
as
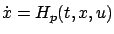 . Thus the joint
evolution of
. Thus the joint
evolution of 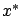 and
and 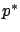 is governed by the system
is governed by the system
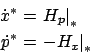 |
(3.39) |
which the reader will recognize as the system of Hamilton's
canonical equations (2.30) from
Section 2.4.1. Let us examine the differential
equation for 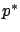 in (3.40) in more detail. We can
expand it with the help of (3.29) as
in (3.40) in more detail. We can
expand it with the help of (3.29) as
where we recall that 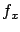 is the Jacobian matrix of
is the Jacobian matrix of 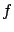 with respect to
with respect to
 . This is a linear time-varying system of the form
. This is a linear time-varying system of the form
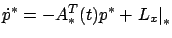 where
where
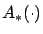 is the same as in
the differential equation (3.28) derived earlier for the
first-order state perturbation
is the same as in
the differential equation (3.28) derived earlier for the
first-order state perturbation 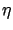 . Two linear systems
. Two linear systems 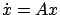 and
and
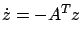 are said to be adjoint
to each other, and for this reason
are said to be adjoint
to each other, and for this reason 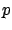 is called the adjoint
vector; the system-theoretic significance of this concept will
become clearer in Section 4.2.8. Note also that we can think of
is called the adjoint
vector; the system-theoretic significance of this concept will
become clearer in Section 4.2.8. Note also that we can think of 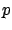 as acting on the
state or, more precisely, on the state velocity vector, since it
always appears inside inner products such as
as acting on the
state or, more precisely, on the state velocity vector, since it
always appears inside inner products such as
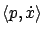 ;
for this reason,
;
for this reason, 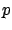 is also called the costate (this
notion will be further explored in
Section 7.1).
is also called the costate (this
notion will be further explored in
Section 7.1).
The purpose of the next two exercises is to recover earlier
conditions from calculus of variations, namely, the Euler-Lagrange equation
and the Lagrange multiplier condition (for multiple degrees of
freedom and several constraints) from the preliminary necessary
conditions for optimality derived so far, expressed by the
existence of an adjoint vector 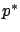 satisfying (3.39)
and (3.40).
satisfying (3.39)
and (3.40).

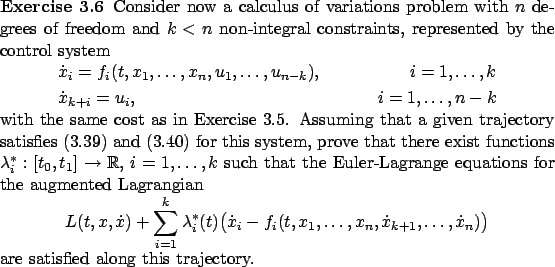
We caution the reader that the transition between the Hamiltonian and the Lagrangian requires some care, especially in the context of Exercise 3.6. The Lagrangian
explicitly depends on 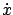 (and the partial derivatives
(and the partial derivatives
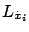 appear in the Euler-Lagrange
equations), whereas the Hamiltonian should
not (it should be a function of
appear in the Euler-Lagrange
equations), whereas the Hamiltonian should
not (it should be a function of 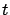 ,
,  ,
,  , and
, and 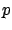 ). The
differential equations can be used to put
). The
differential equations can be used to put 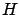 into the right form. A consequence
of this, in Exercise 3.6, is that
into the right form. A consequence
of this, in Exercise 3.6, is that  will appear inside
will appear inside 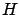 in several
different places.
The Lagrange multipliers
in several
different places.
The Lagrange multipliers
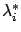 are related to the components of the adjoint vector
are related to the components of the adjoint vector
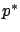 , but they are not the same.
, but they are not the same.





Next: 3.4.3 Second variation
Up: 3.4 Variational approach to
Previous: 3.4.1 Preliminaries
Contents
Index
Daniel
2010-12-20
![]() of the cost functional
of the cost functional ![]() at the optimal control function
at the optimal control function ![]() . To do this, in view of the definition (1.33), we must isolate the first-order terms with respect to
. To do this, in view of the definition (1.33), we must isolate the first-order terms with respect to ![]() in the cost difference between the perturbed control (3.24) and the optimal control
in the cost difference between the perturbed control (3.24) and the optimal control ![]() :
:
![]() for all
for all ![]() .
This condition is true for every function
.
This condition is true for every function ![]() , but becomes
particularly revealing if we make a special choice of
, but becomes
particularly revealing if we make a special choice of ![]() .
Namely, let
.
Namely, let ![]() be
the solution of the differential equation
be
the solution of the differential equation
![]() . Thus the joint
evolution of
. Thus the joint
evolution of ![]() and
and ![]() is governed by the system
is governed by the system
![]() satisfying (3.39)
and (3.40).
satisfying (3.39)
and (3.40).
![]() (and the partial derivatives
(and the partial derivatives
![]() appear in the Euler-Lagrange
equations), whereas the Hamiltonian should
not (it should be a function of
appear in the Euler-Lagrange
equations), whereas the Hamiltonian should
not (it should be a function of ![]() ,
, ![]() ,
, ![]() , and
, and ![]() ). The
differential equations can be used to put
). The
differential equations can be used to put ![]() into the right form. A consequence
of this, in Exercise 3.6, is that
into the right form. A consequence
of this, in Exercise 3.6, is that ![]() will appear inside
will appear inside ![]() in several
different places.
The Lagrange multipliers
in several
different places.
The Lagrange multipliers
![]() are related to the components of the adjoint vector
are related to the components of the adjoint vector
![]() , but they are not the same.
, but they are not the same.