5.1.4 Sufficient condition for optimality

Together, the HJB equation--written as (5.10) or (5.12)--and the Hamiltonian maximization condition (5.14) constitute necessary conditions for optimality. It should be clear that all we proved so far is their necessity. Indeed, defining $V$ to be the value function, we showed that it must satisfy the HJB equation. Assuming further that an optimal control exists, we showed that it must maximize the Hamiltonian along the optimal trajectory. However, we will see next that these conditions are also sufficient for optimality. Namely, we will establish the following sufficient condition for optimality: Suppose that a $\mathcal C^1$ function $\widehat V:[t_0,t_1]\times \mathbb{R}^n\to\mathbb{R}$ satisfies the HJB equation

$$-{\widehat V}_{t}(t,x)=\inf_{u\in U} \big\{L(t,x,u)+\big\langle {... ...,x), f(t,x,u)\big\rangle \big\}% \qquad \foral t\in[t_0,t_1),\ \foral x\in\R^n$$ (5.16)

(for all $t\in[t_0,t_1)$ and all $x\in\mathbb{R}^n$ ) and the boundary condition

$$\widehat V(t_1,x)=K(x).$$ (5.17)

Suppose that a control $\hat u:[t_0,t_1]\to U$ and the corresponding trajectory $\hat x:[t_0,t_1]\to\mathbb{R}^n$ , with the given initial condition $\hat x(t_0)=x_0$ , satisfy everywhere the equation

$$L(t,\hat x(t),\hat u(t))+\big\langle {\widehat V}_{x}(t,\hat x(t)... ...)+\big\langle {\widehat V}_{x}(t,\hat x(t)), f(t,\hat x(t),u)\big\rangle \big\}$$ (5.18)

which is equivalent to the Hamiltonian maximization condition

$$H(t,\hat x(t),\hat u(t),-{\widehat V}_{x}(t,\hat x(t)))=\max_{u\in U} H(t,\hat x(t),u,-{\widehat V}_{x}(t,\hat x(t))).$$

Then $\widehat V(t_0,x_0)$ is the optimal cost (i.e., $\widehat V(t_0,x_0)=V(t_0,x_0)$ where $V$ is the value function) and $\hat u$ is an optimal control. (Note that this optimal control is not claimed to be unique; there can be multiple controls giving the same cost.)

To prove this result, let us first apply (5.20) with $x=\hat x(t)$ . We know from (5.22) that along $\hat x$ , the infimum is a minimum and it is achieved at $\hat u$ ; hence we have, similarly to (5.13),

$$-{\widehat V}_{t}(t,\hat x(t))= L(t,\hat x(t),\hat u(t))+\big\langle {\widehat V}_{x}(t,\hat x(t)),f(t,\hat x(t),\hat u(t))\big\rangle .$$

We can move the ${\widehat V}_{t}$ term to the right-hand side and note that together with the inner product of ${\widehat V}_{x}$ and $f$ it forms the total time derivative of ${\widehat V}$ along $\hat x$ :

$$0=L(t,\hat x(t),\hat u(t))+{\frac{d}{dt}}\,{\widehat V}(t,\hat x(t)).$$

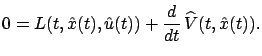
Integrating this equality with respect to $t$ from $t_0$ to $t_1$ , we have

$$0=\int_{t_0}^{t_1} L(t,\hat x(t),\hat u(t))dt+{\widehat V}(t_1,\hat x(t_1)) -{\widehat V}(t_0,\hat x(t_0))$$

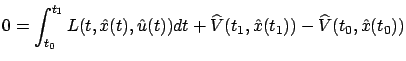
which, in view of the boundary condition for ${\widehat V}$ and the initial condition for $\hat x$ , gives

$${\widehat V}(t_0,x_0)=\int_{t_0}^{t_1} L(t,\hat x(t),\hat u(t))dt+K(\hat x(t_1))=J(t_0,x_0,\hat u).$$ (5.19)

On the other hand, if $x$ is another trajectory with the same initial condition corresponding to an arbitrary control $u$ , then (5.20) implies that

$$-{\widehat V}_{t}(t, x(t))\le L(t, x(t), u(t))+\langle {\widehat V}_{x}(t, x(t)), f(t, x(t), u(t))\rangle$$

or

$$0\le L(t, x(t), u(t))+{\frac{d}{dt}}\,{\widehat V}(t,x(t)).$$

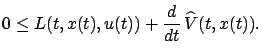
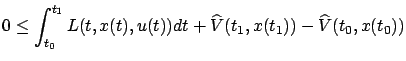
Integrating over $[t_0,t_1]$ as before, we obtain

$$0\le\int_{t_0}^{t_1} L(t, x(t), u(t))dt+{\widehat V}(t_1, x(t_1)) -{\widehat V}(t_0,x(t_0))$$

or

$${\widehat V}(t_0,x_0)\le\int_{t_0}^{t_1} L(t, x(t), u(t))dt+K( x(t_1))=J(t_0,x_0, u).$$ (5.20)

The equation (5.23) and the inequality (5.24) show that $\hat u$ gives the cost ${\widehat V}(t_0,x_0)$ while no other control $u$ can produce a smaller cost. Thus we have confirmed that ${\widehat V}$ is the optimal cost and $\hat u$ is an optimal control.

We can regard the function $\widehat V$ as providing a tool for verifying optimality of candidate optimal controls (obtained, for example, from the maximum principle). This optimality is automatically global. A simple modification of the above argument yields that $\widehat V(t,\hat x(t))$ is the optimal cost-to-go from an arbitrary point $(t,\hat x(t))$ on the trajectory $\hat x$ . More generally, since $\widehat V$ is defined for all $t$ and $x$ , we could use an arbitrary pair $(t,x)$ in place of $(t_0,x_0)$ and obtain optimality with respect to $x(t)=x$ as the initial condition in the same way. Thus, if we have a family of controls parameterized by $(t,x)$ , each fulfilling the Hamiltonian maximization condition along the corresponding trajectory which starts at $x(t)=x$ , then $\widehat V$ is the value function and it lets us establish optimality of all these controls. A typical way in which such a control family can arise is from a state feedback law description; we will encounter a scenario of this kind in Chapter 6. The next two exercises offer somewhat different twists on the above sufficient condition for optimality.