![[*]](crossref.gif) but will instead touch the ground and have
two corner points; see Figure 3.1. Below is another example
in which a corner point arises.
but will instead touch the ground and have
two corner points; see Figure 3.1. Below is another example
in which a corner point arises.
Recall from Section 2.2.1 that a piecewise
![]() curve
curve ![]() on
on ![]() is
is
![]() everywhere except possibly at a finite number of points where it is
continuous but its derivative
everywhere except possibly at a finite number of points where it is
continuous but its derivative ![]() is discontinuous. Such points
of discontinuity of
is discontinuous. Such points
of discontinuity of ![]() are known
as corner points. A corner point
are known
as corner points. A corner point ![]() is characterized by the property
that the left-hand derivative
is characterized by the property
that the left-hand derivative
![]() and the
right-hand derivative
and the
right-hand derivative
![]() both exist but have
different values. For example, if a hanging chain (catenary) is suspended
too close to the ground, then it will not look as in Figure 2.3
on page
both exist but have
different values. For example, if a hanging chain (catenary) is suspended
too close to the ground, then it will not look as in Figure 2.3
on page ![[*]](crossref.gif) but will instead touch the ground and have
two corner points; see Figure 3.1. Below is another example
in which a corner point arises.
but will instead touch the ground and have
two corner points; see Figure 3.1. Below is another example
in which a corner point arises.
Suppose that a piecewise
![]() curve
curve ![]() is a strong extremum
for the Basic Calculus of Variations Problem, under the same assumptions as in Section 2.3.
Clearly,
is a strong extremum
for the Basic Calculus of Variations Problem, under the same assumptions as in Section 2.3.
Clearly, ![]() is then also a weak extremum, with respect to the generalized
1-norm
is then also a weak extremum, with respect to the generalized
1-norm
For simplicity, we
assume that ![]() has only one (unspecified) corner point
has only one (unspecified) corner point
![]() . As a generalization of (2.10), we will let two separate perturbations
. As a generalization of (2.10), we will let two separate perturbations ![]() and
and
![]() act on the two portions of
act on the two portions of ![]() (before and after the
corner point). To make this construction precise, denote these two
portions by
(before and after the
corner point). To make this construction precise, denote these two
portions by
![]() and
and
![]() ; their
perturbed versions will then be
; their
perturbed versions will then be
![]() and
and
![]() . Clearly, we must have
. Clearly, we must have
![]() to preserve the endpoints. Furthermore, since the location of the
corner point is not fixed, we should allow the corner point of the
perturbed curve to deviate from
to preserve the endpoints. Furthermore, since the location of the
corner point is not fixed, we should allow the corner point of the
perturbed curve to deviate from ![]() . Let this new corner point be
. Let this new corner point be
![]() for some
for some
![]() , with the same
, with the same ![]() as
before for convenience. Our family of perturbed curves
(parameterized by
as
before for convenience. Our family of perturbed curves
(parameterized by ![]() ) is thus determined by the two curves
) is thus determined by the two curves
![]() ,
, ![]() and one real number
and one real number
![]() . We label these new curves as
. We label these new curves as
![]() , with
, with
![]() .
There will be an additional condition on
.
There will be an additional condition on ![]() and
and ![]() to
guarantee that
to
guarantee that
![]() is continuous for each
is continuous for each ![]() ;
see (3.4) below. We take both
;
see (3.4) below. We take both ![]() and
and
![]() to be
to be
![]() , to ensure that
, to ensure that
![]() is
piecewise
is
piecewise
![]() with a single corner point at
with a single corner point at
![]() . (Note that the difference
. (Note that the difference
![]() is piecewise
is piecewise
![]() with two corner points, one at
with two corner points, one at ![]() and the other
at
and the other
at
![]() .)
Figure 3.2 should help visualize this situation and the argument
that follows.
.)
Figure 3.2 should help visualize this situation and the argument
that follows.
The reader might have noticed a small problem which we need to fix before proceeding. The domain of ![]() is
is ![]() , whereas we want the domain of
, whereas we want the domain of
![]() to be
to be
![]() . For
. For
![]() , such a perturbed curve is ill defined. To deal with this issue, let us agree to extend
, such a perturbed curve is ill defined. To deal with this issue, let us agree to extend ![]() beyond
beyond ![]() via linear continuation: define
via linear continuation: define ![]() for
for ![]() by
by
![]() . The linearity is actually not crucial,
all we need is that the function
. The linearity is actually not crucial,
all we need is that the function ![]() be
be
![]() at
at
![]() , with
, with
Let us write the functional to be minimized as a sum of two components:
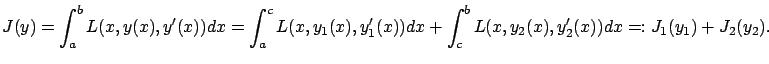
After the perturbation, the first functional becomes
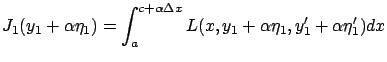
(note that
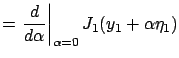 |
||
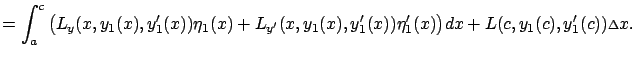 |
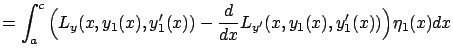 |
||
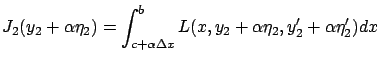
and the first variation of
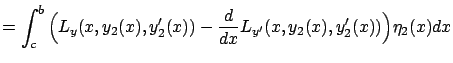 |
||
For ![]() close to 0, the perturbed curve
close to 0, the perturbed curve
![]() is close to the original curve
is close to the original curve ![]() in the sense of the 0-norm.
Therefore, the function
in the sense of the 0-norm.
Therefore, the function
![]() must attain a minimum at
must attain a minimum at ![]() , implying that
, implying that
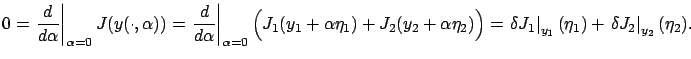
Next, observe that each of the two portions
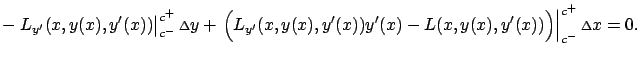 |
The above reasoning can be extended to multiple corner points,
yielding the necessary conditions for optimality known as the
Weierstrass-Erdmann corner conditions: If a
curve ![]() is a strong extremum, then
is a strong extremum, then
![]() and
and
![]() must be continuous at each corner point
of
must be continuous at each corner point
of ![]() .
More precisely, their discontinuities (due to the fact that
.
More precisely, their discontinuities (due to the fact that ![]() does not exist at corner points) must be removable.
The quantities
does not exist at corner points) must be removable.
The quantities ![]() and
and
![]() are of course familiar to us from Chapter 2;
they are, respectively, the momentum and the Hamiltonian.
Weierstrass presented these conditions in 1865
during his lectures on calculus of
variations, but never formally published them.
They were independently derived and published by Erdmann in
1877.
are of course familiar to us from Chapter 2;
they are, respectively, the momentum and the Hamiltonian.
Weierstrass presented these conditions in 1865
during his lectures on calculus of
variations, but never formally published them.
They were independently derived and published by Erdmann in
1877.
For the case of a single corner point,
the two Weierstrass-Erdmann corner conditions
together with the two boundary
conditions provide four relations, which is
the correct number to uniquely specify two portions
of the extremal (each satisfying the second-order Euler-Lagrange differential equation).
In general, to uniquely specify an extremal
consisting
of ![]() portions (i.e., having
portions (i.e., having ![]() corner points) we need
corner points) we need ![]() conditions,
and these are provided by
conditions,
and these are provided by ![]() corner conditions plus the
two boundary conditions.
corner conditions plus the
two boundary conditions.
