2.1.3 Catenary

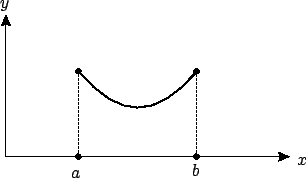
Suppose that a chain of a given length, with uniform mass density, is suspended freely between two fixed points (see Figure 2.3). What will be the shape of this chain? This question was posed by Galileo in the 1630s, and he claimed--incorrectly--that the solution is a parabola.

Figure: A catenary

Mathematically, the chain is described by a continuous function $y:[a,b]\to [0,\infty)$ , and the two suspension points are specified by endpoint constraints of the form $y(a)=y_0$ , $y(b)=y_1$ . The length constraint is again given by (2.1). In the figure we took $y_0$ and $y_1$ to be equal, and also assumed that the suspension points are high enough and far enough apart compared to the length $C_0$ so that the chain does not touch the ground ($y(x)>0$ for all $x$ ). The chain will take the shape of minimal potential energy. This amounts to saying that the $y$ -coordinate of its center of mass should be minimized. Since the mass density is uniform, we integrate the $y$ -coordinate of the point along the curve with respect to the arclength and obtain the functional

$$J(y)=\int_a^b y(x) \sqrt{1+(y'(x))^2}dx$$

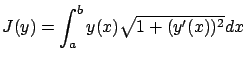
(the actual center of mass is $J(y)/C_0$ ). Thus the problem is to minimize this functional subject to the length constraint (2.1). As in Dido's problem, we need to assume that $y$ is differentiable (at least almost everywhere); this time we do it also to ensure that the cost is well defined, because $y'$ appears inside the integral in $J$ .

The correct description of the catenary curve was obtained by Johann Bernoulli in 1691. It is given by the formula

$$y(x)=c \cosh (x/c), \qquad c>0$$ (2.3)

(modulo a translation of the origin in the $(x,y)$ -plane), unless the chain is suspended too low and touches the ground. The name ``catenary" is derived from the Latin word catena (chain).