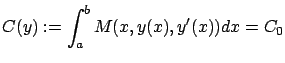 |
(2.44) |
Suppose that we augment the Basic Calculus of Variations Problem with an additional constraint of the form
Assume that a given curve ![]() is an extremum.
What follows is a heuristic argument motivated by our earlier
derivation of the first-order
necessary condition for constrained optimality in the finite-dimensional case
(involving Lagrange multipliers).
Let us consider perturbed curves of the familiar form
is an extremum.
What follows is a heuristic argument motivated by our earlier
derivation of the first-order
necessary condition for constrained optimality in the finite-dimensional case
(involving Lagrange multipliers).
Let us consider perturbed curves of the familiar form
To be admissible, the perturbation
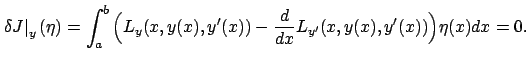
This conclusion can be summarized as follows:
![[*]](crossref.gif) . It also has a similar consequence, namely, that
there exists a constant
. It also has a similar consequence, namely, that
there exists a constant
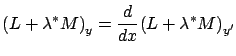
which amounts to saying that the Euler-Lagrange equation holds for the augmented Lagrangian
A closer inspection of the above argument reveals, however,
that we left a couple of gaps.
First, we did not justify the step of passing from (2.48)
to (2.49). In the finite-dimensional case, we had to make
the corresponding step of passing from (1.21)
to (1.22) which then gave (1.25); we
would need to construct a similar reasoning here, treating the integrals
in (2.48) as inner products of ![]() with the functions in parentheses
(inner products in
with the functions in parentheses
(inner products in
![]() ). Second, there was actually
a more serious logical flaw: the condition (2.46) is necessary
for
the perturbation
). Second, there was actually
a more serious logical flaw: the condition (2.46) is necessary
for
the perturbation ![]() to preserve the constraint (2.45),
but we do not know whether
it is sufficient. Without this sufficiency, the validity of (2.48) is
in serious doubt. In the finite-dimensional case, to reach (1.21)
we used the fact that (1.20) was a necessary and sufficient
condition for
to preserve the constraint (2.45),
but we do not know whether
it is sufficient. Without this sufficiency, the validity of (2.48) is
in serious doubt. In the finite-dimensional case, to reach (1.21)
we used the fact that (1.20) was a necessary and sufficient
condition for ![]() to be a tangent vector; we did not, however, give a proof
of the sufficiency part (which is not trivial).
to be a tangent vector; we did not, however, give a proof
of the sufficiency part (which is not trivial).
It is also important to recall that in the finite-dimensional case studied
in Section 1.2.2, the first-order
necessary condition for constrained optimality in terms of Lagrange multipliers
is valid only when an additional technical assumption holds, namely,
the extremum must be a regular point of the constraint surface. This assumption
is needed to rule out degenerate situations (see Exercise 1.2);
in fact,
it enables precisely the sufficiency part
mentioned in the previous paragraph. It turns out that in the present case,
a degenerate situation
arises when the test curve ![]() satisfies the constraint but all nearby
curves violate it. This can happen if
satisfies the constraint but all nearby
curves violate it. This can happen if ![]() is an extremal of the constraint functional
is an extremal of the constraint functional ![]() ,
i.e., satisfies the Euler-Lagrange equation for
,
i.e., satisfies the Euler-Lagrange equation for ![]() . For example, consider the
length constraint
. For example, consider the
length constraint
![]() together with the boundary conditions
together with the boundary conditions
![]() . Clearly,
. Clearly, ![]() is the only admissible curve
(it is the unique global minimum
of the constraint functional),
hence it automatically solves our constrained problem no matter what
is the only admissible curve
(it is the unique global minimum
of the constraint functional),
hence it automatically solves our constrained problem no matter what ![]() is.
The
second integral in (2.48) is 0 for every
is.
The
second integral in (2.48) is 0 for every
![]() since
since ![]() is an extremal of
is an extremal of ![]() .
Thus if (2.48) were true, it would imply that
.
Thus if (2.48) were true, it would imply that
![]() must be an extremal of
must be an extremal of ![]() , but as we just explained this is not necessary.
We see that if we hope for (2.48) to be a necessary condition for
constrained optimality, we need to assume that
, but as we just explained this is not necessary.
We see that if we hope for (2.48) to be a necessary condition for
constrained optimality, we need to assume that ![]() is not an extremal of
is not an extremal of ![]() ,
so that there exist nearby curves at which
,
so that there exist nearby curves at which ![]() takes values both larger
and smaller than
takes values both larger
and smaller than ![]() .
.
We can now conjecture the following first-order necessary
condition for constrained optimality: If ![]() is an extremum for the
constrained problem and is not an
extremal of the constraint functional
is an extremum for the
constrained problem and is not an
extremal of the constraint functional ![]() (i.e., does
not satisfy the Euler-Lagrange equation for
(i.e., does
not satisfy the Euler-Lagrange equation for ![]() ), then it is an extremal of
the augmented cost functional (2.50) for some
), then it is an extremal of
the augmented cost functional (2.50) for some
![]() .
We can also state this condition more succinctly, combining
the nondegeneracy assumption and the conclusion into one statement:
.
We can also state this condition more succinctly, combining
the nondegeneracy assumption and the conclusion into one statement: ![]() must
satisfy the Euler-Lagrange equation for
must
satisfy the Euler-Lagrange equation for
![]() ,
where
,
where
![]() and
and ![]() are constants (not both 0). Indeed,
this means that either
are constants (not both 0). Indeed,
this means that either
![]() and
and ![]() is an extremal of
is an extremal of ![]() , or
, or
![]() and
and
![]() is an extremal of
is an extremal of
![]() .
The number
.
The number
![]() is called the abnormal multiplier (it also has
an analog
in optimal control which will appear in Section 4.1).
is called the abnormal multiplier (it also has
an analog
in optimal control which will appear in Section 4.1).
It turns out that this conjecture is correct. However, rather than fixing the above faulty argument, it is easier to give an alternative proof by proceeding along the lines of the second proof in Section 1.2.2.

In the unconstrained case, as we noted earlier, the general solution of the
second-order Euler-Lagrange differential
equation depends on two arbitrary constants whose values are to be determined
from the two boundary conditions. Here we have one additional parameter
![]() but also one additional constraint (2.45),
so generically
we still expect to obtain a unique extremal.
but also one additional constraint (2.45),
so generically
we still expect to obtain a unique extremal.
The generalization of the above necessary condition to problems with several constraints is straightforward: we need one Lagrange multiplier for each constraint (cf. Section 1.2.2). The multiple-degrees-of-freedom setting also presents no complications.
Similarly to the finite-dimensional case, Lagrange's original intuition
was to replace constrained minimization of ![]() with
respect to
with
respect to ![]() by
unconstrained minimization of
by
unconstrained minimization of
![[*]](crossref.gif) ,
considering this augmented cost (which matches (2.50) except
for an additive constant) does not lead to a rigorous justification of
the necessary condition.
,
considering this augmented cost (which matches (2.50) except
for an additive constant) does not lead to a rigorous justification of
the necessary condition.
Equipped with the above necessary condition for the case of integral constraints as well as our previous experience with the Euler-Lagrange equation, we can now study Dido's isoperimetric problem and the catenary problem.