| (3.17) |
In the notation announced at the end of the previous section, control systems that we want to study take the form
We want to know that for every choice of the initial data
![]() and every admissible control
and every admissible control ![]() , the
system (3.18) has a unique solution
, the
system (3.18) has a unique solution ![]() on
some time interval
on
some time interval ![]() . If this property holds, we will
say that the system is well posed.
To guarantee local existence and uniqueness
of solutions for (3.18), we need to impose some regularity
conditions on the right-hand side
. If this property holds, we will
say that the system is well posed.
To guarantee local existence and uniqueness
of solutions for (3.18), we need to impose some regularity
conditions on the right-hand side ![]() and on the admissible controls
and on the admissible controls ![]() .
For the sake of simplicity, we will usually
be willing to make slightly stronger assumptions than necessary; when we do this,
we will briefly indicate how our assumptions can be relaxed.
.
For the sake of simplicity, we will usually
be willing to make slightly stronger assumptions than necessary; when we do this,
we will briefly indicate how our assumptions can be relaxed.
Let us first consider the case of no controls:
Second, we need to specify how regular ![]() should be with respect to
should be with respect to ![]() .
A standard assumption in this regard is that
.
A standard assumption in this regard is that
![]() is locally
Lipschitz in
is locally
Lipschitz in ![]() , uniformly over
, uniformly over ![]() . Namely, for every
. Namely, for every ![]() there should exist a constant
there should exist a constant ![]() such that we have
such that we have
for all
If ![]() satisfies the above regularity assumptions,
then on some interval
satisfies the above regularity assumptions,
then on some interval ![]() there exists a unique solution
there exists a unique solution
![]() of the system (3.19). Since we did not assume that
of the system (3.19). Since we did not assume that
![]() is continuous with respect to
is continuous with respect to ![]() , some care is needed in interpreting
what we mean by a solution of (3.19). In the present situation,
it is reasonable to call a function
, some care is needed in interpreting
what we mean by a solution of (3.19). In the present situation,
it is reasonable to call a function
![]() a solution of (3.19) if it
is continuous everywhere,
a solution of (3.19) if it
is continuous everywhere,
![]() almost everywhere, and satisfies the corresponding integral equation
almost everywhere, and satisfies the corresponding integral equation
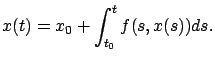
A function
We are now ready to go back to the control system (3.18).
To guarantee local existence and uniqueness of its solutions, we can impose
assumptions on ![]() and
and ![]() that would let us invoke the previous existence and
uniqueness result for the right-hand side
that would let us invoke the previous existence and
uniqueness result for the right-hand side
for all

When the right-hand side does not explicitly depend on time, i.e., when
we have ![]() , a convenient way to guarantee that the above conditions
hold is to assume that
, a convenient way to guarantee that the above conditions
hold is to assume that ![]() is locally Lipschitz (as a function from
is locally Lipschitz (as a function from
![]() to
to
![]() ).
In general,
).
In general, ![]() depends on
depends on ![]() in two ways: directly through the
in two ways: directly through the
![]() argument, and indirectly through
argument, and indirectly through ![]() . Regarding the first dependence,
we are willing to be generous by assuming that
. Regarding the first dependence,
we are willing to be generous by assuming that ![]() is at least continuous in
is at least continuous in ![]() .
In fact, we can always eliminate the direct dependence of
.
In fact, we can always eliminate the direct dependence of ![]() on
on ![]() by introducing the extra state variable
by introducing the extra state variable
![]() , with the dynamics
, with the dynamics
![]() . Note that in order for the new system obtained in this way
to satisfy our conditions for existence and uniqueness of
solutions, continuity of
. Note that in order for the new system obtained in this way
to satisfy our conditions for existence and uniqueness of
solutions, continuity of ![]() in
in ![]() is not enough and we need
is not enough and we need ![]() to be
to be
![]() in
in ![]() (or satisfy
an appropriate Lipschitz condition).
(or satisfy
an appropriate Lipschitz condition).
On the other hand, as far as regularity of ![]() with
respect to
with
respect to ![]() is concerned, it would be too restrictive to assume
anything stronger than piecewise continuity.
In fact, occasionally we may even want to relax this assumption and
allow
is concerned, it would be too restrictive to assume
anything stronger than piecewise continuity.
In fact, occasionally we may even want to relax this assumption and
allow ![]() to be a locally bounded function with countably many
discontinuities. More precisely, the class of admissible
controls can be defined to consist of functions
to be a locally bounded function with countably many
discontinuities. More precisely, the class of admissible
controls can be defined to consist of functions
![]() that are measurable3.2 and locally
bounded. In view of the remarks made earlier about
the system (3.19), local existence and uniqueness of solutions is
still guaranteed for this larger class
of controls.
We will rarely need this level of generality, and piecewise continuous controls will be adequate for most of our
purposes (with the exception of some of the material to be
discussed in Sections 4.4
and 4.5--specifically, Fuller's problem
and Filippov's theorem). Similarly to the case of the
system (3.19), by a solution of (3.18) we
mean an absolutely continuous function
that are measurable3.2 and locally
bounded. In view of the remarks made earlier about
the system (3.19), local existence and uniqueness of solutions is
still guaranteed for this larger class
of controls.
We will rarely need this level of generality, and piecewise continuous controls will be adequate for most of our
purposes (with the exception of some of the material to be
discussed in Sections 4.4
and 4.5--specifically, Fuller's problem
and Filippov's theorem). Similarly to the case of the
system (3.19), by a solution of (3.18) we
mean an absolutely continuous function ![]() satisfying
satisfying
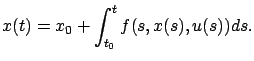
In what follows, we will always assume that the property of local existence and uniqueness of solutions holds for a given control system. This of course does not guarantee that solutions exist globally in time. Typically, we will consider a candidate optimal trajectory defined on some time interval
![]() , and then existence over the same time interval will be automatically ensured for nearby trajectories.
, and then existence over the same time interval will be automatically ensured for nearby trajectories.