




Next: 4.3.1.4 Initial sets
Up: 4.3.1 Changes of variables
Previous: 4.3.1.2 Time-dependent system and
Contents
Index
4.3.1.3 Terminal cost
Let us now consider a situation where a terminal cost of the form
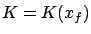 is present. To illustrate just one simple case, we
suppose that we are dealing with a free-time, free-endpoint
problem in the Mayer form, i.e., there is no running
cost (
is present. To illustrate just one simple case, we
suppose that we are dealing with a free-time, free-endpoint
problem in the Mayer form, i.e., there is no running
cost (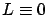 ). We assume the function
). We assume the function 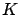 to be differentiable as many times as desired;
everything else is as in the Basic
Variable-Endpoint Control Problem.
to be differentiable as many times as desired;
everything else is as in the Basic
Variable-Endpoint Control Problem.
Since 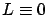 , there is no need to consider the
, there is no need to consider the 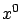 -coordinate. Temporal and spatial control
perturbations can be used to construct the terminal cone
-coordinate. Temporal and spatial control
perturbations can be used to construct the terminal cone 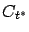 as
before, except that it now lives in the original
as
before, except that it now lives in the original  -space:
-space:
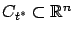 . By optimality, and since the terminal state is free, no
perturbed state
trajectory can have a terminal cost lower than
. By optimality, and since the terminal state is free, no
perturbed state
trajectory can have a terminal cost lower than
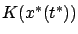 , the terminal cost
of the candidate optimal trajectory. Thus we expect that
, the terminal cost
of the candidate optimal trajectory. Thus we expect that 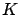 should not decrease along any direction in
should not decrease along any direction in 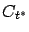 , a property that
we can write as
, a property that
we can write as
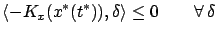 such that such that 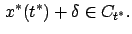 |
(4.42) |
Geometrically, this means that 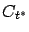 lies on one side of the
hyperplane passing through
lies on one side of the
hyperplane passing through 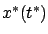 with normal
with normal
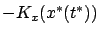 , which we henceforth assume to be a nonzero vector.
A comparison of (4.42) with (4.29)
unmistakably suggests that we should define
, which we henceforth assume to be a nonzero vector.
A comparison of (4.42) with (4.29)
unmistakably suggests that we should define
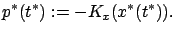 |
(4.43) |
Indeed, we know that in a
free-endpoint problem the final value of the costate should be
completely constrained (to give the correct total number of
boundary conditions for the system of canonical equations). With
the above definition of 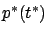 the
inequality (4.42) matches (4.29), following
which the adjoint equation and the analysis of the
Hamiltonian
the
inequality (4.42) matches (4.29), following
which the adjoint equation and the analysis of the
Hamiltonian
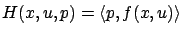 |
(4.44) |
are developed in the same fashion as before. The
companion inequality (4.30) in our earlier proof of the
maximum principle was only needed to show that
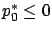 ; here
we do not have such an inequality, and we do not need it because
there is no
; here
we do not have such an inequality, and we do not need it because
there is no 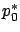 .
.
The above argument is of course not rigorous, so let us again
validate our conjecture by formally reducing the present scenario
to the Basic Variable-Endpoint Control Problem. A transformation
that accomplishes this goal is provided by the formula
Ignoring 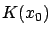 which is a known constant, we arrive at an
equivalent problem in the Lagrange form with
which is a known constant, we arrive at an
equivalent problem in the Lagrange form with
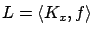 . For this modified problem, the Hamiltonian
is
. For this modified problem, the Hamiltonian
is
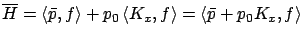 where
where 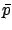 is the costate. Applying the maximum principle, we
obtain the differential equation
is the costate. Applying the maximum principle, we
obtain the differential equation
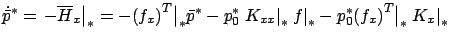 with the boundary condition
with the boundary condition
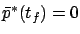 . The latter tells us, by the way, that
. The latter tells us, by the way, that
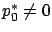 , hence from now on we assume
, hence from now on we assume 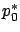 and
and 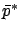 to have
been normalized so that
to have
been normalized so that 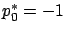 . Now, matching the expression
for
. Now, matching the expression
for
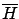 with (4.44), let us define the costate for our original problem to be
with (4.44), let us define the costate for our original problem to be
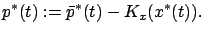 |
(4.45) |
Its final value is
consistent with (4.43). We can check that 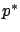 defined in this way satisfies the correct canonical equation.
defined in this way satisfies the correct canonical equation.
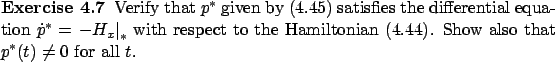
By construction, 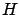 is maximized and equals 0 along the optimal
trajectory because these properties hold for
is maximized and equals 0 along the optimal
trajectory because these properties hold for
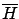 . We
thus conclude that the statement of the maximum principle for the
present case, with respect to the Hamiltonian (4.44), is
obtained from that for the Basic Variable-Endpoint Control Problem
by eliminating
. We
thus conclude that the statement of the maximum principle for the
present case, with respect to the Hamiltonian (4.44), is
obtained from that for the Basic Variable-Endpoint Control Problem
by eliminating 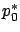 and changing the transversality condition
to
and changing the transversality condition
to
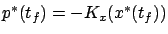 . Recall that we already saw such a boundary condition for the costate in (3.37).
. Recall that we already saw such a boundary condition for the costate in (3.37).





Next: 4.3.1.4 Initial sets
Up: 4.3.1 Changes of variables
Previous: 4.3.1.2 Time-dependent system and
Contents
Index
Daniel
2010-12-20
![]() , there is no need to consider the
, there is no need to consider the ![]() -coordinate. Temporal and spatial control
perturbations can be used to construct the terminal cone
-coordinate. Temporal and spatial control
perturbations can be used to construct the terminal cone ![]() as
before, except that it now lives in the original
as
before, except that it now lives in the original ![]() -space:
-space:
![]() . By optimality, and since the terminal state is free, no
perturbed state
trajectory can have a terminal cost lower than
. By optimality, and since the terminal state is free, no
perturbed state
trajectory can have a terminal cost lower than
![]() , the terminal cost
of the candidate optimal trajectory. Thus we expect that
, the terminal cost
of the candidate optimal trajectory. Thus we expect that ![]() should not decrease along any direction in
should not decrease along any direction in ![]() , a property that
we can write as
, a property that
we can write as
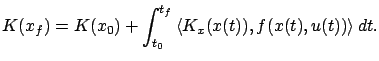
![]() is maximized and equals 0 along the optimal
trajectory because these properties hold for
is maximized and equals 0 along the optimal
trajectory because these properties hold for
![]() . We
thus conclude that the statement of the maximum principle for the
present case, with respect to the Hamiltonian (4.44), is
obtained from that for the Basic Variable-Endpoint Control Problem
by eliminating
. We
thus conclude that the statement of the maximum principle for the
present case, with respect to the Hamiltonian (4.44), is
obtained from that for the Basic Variable-Endpoint Control Problem
by eliminating ![]() and changing the transversality condition
to
and changing the transversality condition
to
![]() . Recall that we already saw such a boundary condition for the costate in (3.37).
. Recall that we already saw such a boundary condition for the costate in (3.37).