7.1.1 Differentiable manifolds

We say that $M$ is a $k$ -dimensional differentiable manifold embedded in $\mathbb{R}^n$ , or simply a manifold, if it is given by

$$M=\{x\in\mathbb{R}^n: h_1(x)=h_2(x)=\dots=h_{n-k}(x)=0\}$$ (7.1)

where $h_i$ , $i=1, \dots, n-k$ are $\mathcal C^1$ functions from $\mathbb{R}^n$ to $\mathbb{R}$ such that the gradient vectors $\nabla h_i(x)$ , $i=1, \dots, n-k$ are linearly independent for each $x\in M$ . This is actually not a new object for us: it is just a $k$ -dimensional surface in $\mathbb{R}^n$ already considered in Section 1.2.2 and later in the formulation of the Basic Variable-Endpoint Control Problem in Chapter 4. The linear independence assumption imposed on the gradients means, in the terminology of Section 1.2.2, that all points of $M$ are regular.

Intuitively speaking, a $k$ -dimensional manifold $M$ is a subset of $\mathbb{R}^n$ that locally ``looks like" $\mathbb{R}^k$ . This idea can be made precise by equipping $M$ with local coordinates, as follows. Fix an arbitrary $x\in M$ . Since by assumption the (nonsquare) Jacobian matrix

$$\begin{pmatrix}{(h_1)}_{x_1}(x)&\cdots&{(h_1)}_{x_n}(x)\\ \vdots&\ddots&\vdots\\ {(h_{n-k})}_{x_1}(x)&\cdots&{(h_{n-k})}_{x_n}(x) \end{pmatrix}$$

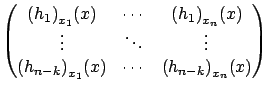
is of rank $n-k$ , it has $n-k$ linearly independent columns; shuffling the variables $x_1,\dots,x_n$ if necessary, we can assume that these are the last $n-k$ columns. Using the Implicit Function Theorem, we can then solve the equations in (7.1) for the variables $x_{k+1},\dots,x_n$ in terms of $x_1,\dots,x_k$ in some neighborhood of $x$ . Consequently, the components $x_1,\dots,x_k$ can be used to describe points in $M$ near $x$ , i.e., they provide a local coordinate chart for $M$ . A simple example of a 1-dimensional manifold in $\mathbb{R}^2$ is the unit circle, for which we invite the reader to work out the above construction.

The standard definition of a manifold is actually stated in terms of the existence of local coordinate charts satisfying suitable compatibility conditions, without any explicit reference to the ambient space $\mathbb{R}^n$ . However, it is known that every manifold defined in this way can be embedded in $\mathbb{R}^n$ for some $n$ large enough. The above more concrete notion of an embedded manifold is sufficient for our purposes, but the concept of local coordinates will be useful for us as well. Basically, we have the choice of representing points in $M$ as $n$ -vectors or locally as $k$ -vectors (cf. the discussion of holonomic constraints in Section 2.5.2).

Let $M$ be a $k$ -dimensional manifold. We know that at each point $x\in M$ we can define the tangent space $T_xM$ (see page ). This is a $k$ -dimensional linear vector space, spanned by the tangent vectors associated with all possible curves in $M$ passing through $x$ . Recall that for a curve $x(\cdot)$ lying in $M$ , with $x(0)=x$ , the corresponding tangent vector is $\dot x(0)$ . In local coordinates, if the curve has components $x_1(\cdot),\dots,x_k(\cdot)$ then the components of the tangent vector $\xi=\dot x(0)$ are $(\xi_1,\dots,\xi_k)=(\dot x_1(0),\dots,\dot x_k(0))$ . It is also useful to consider the union

$$TM:=\bigcup_{x\in M} T_x M$$

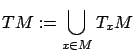
which is called the tangent bundle of $M$ . This is a manifold of dimension $2k$ . We note that in general, $TM$ is not globally diffeomorphic to the direct product $M\times \mathbb{R}^k$ (well-known counterexamples are obtained by taking $M$ to be the two-dimensional sphere or the Mobius band). It is convenient to think of vector fields on $M$ as sections of the tangent bundle, i.e., functions $f:M\to TM$ such that $f(x)\in T_x M$ for all $x$ .

Given a point $x$ on a manifold $M$ , the linear vector space of linear $\mathbb{R}$ -valued functions on $T_xM$ is called the cotangent space to $M$ at $x$ , and is denoted by $T_x^* M$ . This is the dual space^7.1 to $T_xM$ ; its elements are called cotangent vectors, or simply covectors. The simplest example of a covector is the differential of a function. Let $g: M\to \mathbb{R}$ be a $\mathcal C^1$ function. For each $x\in M$ , the linear function $\left.dg\right\vert _{x}: T_x M\to \mathbb{R}$ is defined as follows. Given a tangent vector $\xi\in T_x M$ and an arbitrary curve $x(\cdot)$ in $M$ with $x(0)=x$ having $\xi$ as its tangent vector (so that $\dot x(0)=\xi$ ), let

$$\left.dg\right\vert _{x}(\xi):=\left.\frac{d}{d\alpha}\right\vert _{\alpha=0} g(x(\alpha)).$$

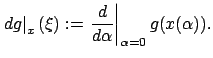
In local coordinates this is given by $\left.dg\right\vert _{x}(\xi)=\sum_{i=1}^k {g}_{x_i}(x)\dot x_i(0)=\sum_{i=1}^k {g}_{x_i}(x)\xi_i$ , which clearly does not depend on the choice of a specific curve $x(\cdot)$ . The map $\left.dg\right\vert _{x}$ assigns to each tangent vector $\xi$ the derivative of $g$ in the direction of $\xi$ . If $x_1,\dots,x_k$ are local coordinates on $M$ , then the corresponding differentials $dx_1, \dots, dx_k$ form a basis for $T_x^* M$ and hence yield local coordinates on the cotangent space. For a tangent vector $\xi\in T_x M$ , the numbers $dx_i(\xi)$ give the components $\xi_i$ of $\xi$ . One also defines the cotangent bundle

$$T^*M=\bigcup_{x\in M} T^*_x M$$

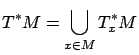
which is itself a manifold, of dimension $2k$ . Combining local coordinates $x_1,\dots,x_k$ on $M$ with local coordinates on $T_x^* M$ relative to the basis given by $dx_1, \dots, dx_k$ , one obtains local coordinates on the cotangent bundle $T^* M$ known as canonical coordinates.