The separation property (4.29) applies, in particular, to
![]() , the terminal state perturbation vector corresponding to a temporal perturbation of the control. We know from (4.9) and (4.7) that this vector is given by
, the terminal state perturbation vector corresponding to a temporal perturbation of the control. We know from (4.9) and (4.7) that this vector is given by
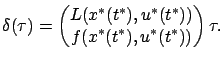
Since
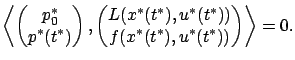
By virtue of (4.8), this is equivalent to
In other words,
Let us show that
![]() is a
continuous function of time, even though the optimal control
is a
continuous function of time, even though the optimal control
![]() need not be continuous. The argument that follows is very
similar to the one that the reader presumably used a while ago to
solve Exercise 3.3 on page
need not be continuous. The argument that follows is very
similar to the one that the reader presumably used a while ago to
solve Exercise 3.3 on page ![[*]](crossref.gif) . Let
. Let ![]() be a
point of discontinuity of
be a
point of discontinuity of ![]() . Of course,
. Of course, ![]() and
and ![]() are
continuous everywhere. Applying the Hamiltonian maximization
condition (4.35) with
are
continuous everywhere. Applying the Hamiltonian maximization
condition (4.35) with ![]() and
and
![]() and making
and making
![]() approach
approach ![]() from the left, we have
from the left, we have
Similarly, applying (4.35) with
Thus the two quantities must actually be equal, and the continuity claim is established.
Next, let us show that the function
![]() is constant. In
Section 3.4.4, in the context of the
variational approach, we established this property by simply
differentiating the Hamiltonian with respect to time, but here we
need to be more careful because the existence of
is constant. In
Section 3.4.4, in the context of the
variational approach, we established this property by simply
differentiating the Hamiltonian with respect to time, but here we
need to be more careful because the existence of ![]() has not
been assumed. In view of the Hamiltonian maximization condition,
we can write
has not
been assumed. In view of the Hamiltonian maximization condition,
we can write
where
We just saw that
![[*]](crossref.gif) ). We can now study its derivative.
). We can now study its derivative.
We have shown that the function
![]() equals 0 at
equals 0 at ![]() ,
is continuous everywhere,
and has zero derivative almost everywhere.
Thus it is identically 0, as claimed. Our proof of the maximum principle for the Basic Fixed-Endpoint Control Problem is now complete. At this point the reader should also finish Exercise 4.2.
,
is continuous everywhere,
and has zero derivative almost everywhere.
Thus it is identically 0, as claimed. Our proof of the maximum principle for the Basic Fixed-Endpoint Control Problem is now complete. At this point the reader should also finish Exercise 4.2.